Seven Deadly Sin-tors Sangaku
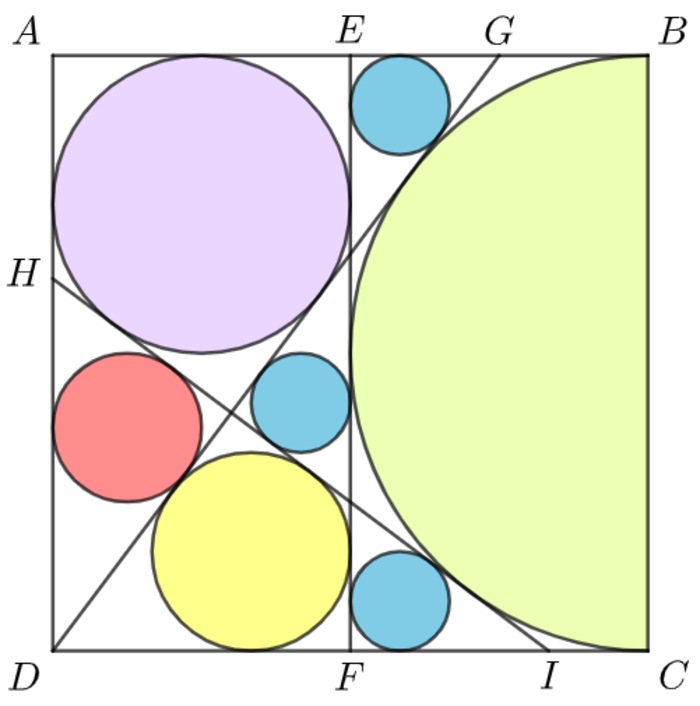
In the square A B C D , E and F are midpoints of A B and C D respectively. Points G , H , and I are selected on the square perimeter, such that the green semicircle and violet and yellow circles are tangent to E F , D G , and H I , which form one red incircle and three identical blue incircles.
If the ratio of the sum of all six smaller radii to the radius of the green semicircle can be expressed as b a , where a and b are coprime positive integers, input a + b as your answer.
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I did get the inradius but I can’t understand which formula you have used to find the inradius of the yellow circle
I had used the area/semi perimeter formula
Is that a general formula or just a specific one to right triangles?
Log in to reply
The inradius of a right triangle is r = 2 1 ( a + b − c ) , where a and b are the legs and c is the hypotenuse. This specific case for right triangles can be derived from area/semi-perimeter formula: r = s A = 2 s 2 A = a + b + c a b = ( a + b + c ) ( a + b − c ) a b ( a + b − c ) = a 2 + 2 a b + b 2 − c 2 a b ( a + b − c ) = 2 a b a b ( a + b − c ) = 2 1 ( a + b − c ) .
Log in to reply
Thanks a lot, this is gonna be very helpful for my competitive exams
By observation, we note that all the triangles are similar right triangles. Let the radius of the green semicircle be r s e m i c i r c l e = 1 . Then the side length of the square is 2 and the radius of the violet circle is r v i o l e t = 2 1 . Since the violet circle is the incircle of △ A G D , from Δ = s r , where Δ is the area of the triangle, s , its semiperimeter and r , the inradius, we have:
2 A D ⋅ A G 2 x 3 x − 2 9 x 2 − 1 2 x + 4 8 x 2 − 1 2 x 2 x − 3 ⟹ x = 2 A D + A G + G D ⋅ 2 1 = 2 2 + x + 4 + x 2 = 4 + x 2 = 4 + x 2 = 0 = 0 = 2 3 = A G Let A G = x Squaring both sides Since x > 0
Now we note that △ A G D is a 3 : 4 : 5 right triangle. This means that all the other similar triangles are also 3 : 4 : 5 right triangles, and this makes calculations easy. And the ratio of the inradius to the side lengths of the triangle is 1 : 3 : 4 : 5 .
r b l u e r y e l l o w r r e d = 3 E G = 3 A G − A E = 3 2 3 − 1 = 6 1 = 5 D I = 5 D F + F I = 5 1 + 3 4 ⋅ E G = 5 1 + 3 4 ⋅ 2 1 = 3 1 = 5 H D = 5 4 3 ⋅ D I = 5 4 3 ⋅ 3 5 = 4 1
Therefore r s e m i c i r c l e r v i o l e t + r y e l l o w + r r e d + 3 r b l u e = 1 2 1 + 3 1 + 4 1 + 3 ⋅ 6 1 = 1 2 1 9 , ⟹ a + b = 1 9 + 1 2 = 3 1 .
Let the sides of the square be 2 , so that the radius the of the green semicircle is r g = 1 and the radius of the violet circle is r v = 2 1 , and label some more points as follows:
△ D M C ≅ △ D M L by HL congruency, so let θ = ∠ L D M = ∠ M D C .
From △ D M C , tan θ = 2 1 , so tan 2 θ = 1 − tan 2 θ 2 tan θ = 1 − ( 2 1 ) 2 2 ⋅ 2 1 = 3 4 , and since ∠ K D F = 2 θ and D F = 1 , K F = 3 4 .
By the Pythagorean Theorem on △ K D F , K D = D F 2 + K F 2 = 1 2 + ( 3 4 ) 2 = 3 5 , so the radius of the yellow circle is r y = 2 1 ( 1 + 3 4 − 3 5 ) = 3 1 .
E K = E F − K F = 2 − 3 4 = 3 2 . Since △ E K G ∼ △ F K D by AA similarity, the radius of the blue circle is r b = K F E K ⋅ r y = 3 4 3 2 ⋅ 3 1 = 6 1 .
Since △ E K G ∼ △ J K N by AA similarity and the blue incircles are identical, △ E K G ≅ △ J K N and J K = K E = 3 2 .
That means D J = D K − J K = 3 5 − 3 2 = 1 .
Since △ J D H ∼ △ F K D by AA similarity, the radius of the red circle is r r = K F D J ⋅ r y = 3 4 1 ⋅ 3 1 = 4 1 .
That means the ratio of the sum of all six smaller radii to the radius of the green semicircle is r g 3 r b + r v + r y + r r = 1 3 ⋅ 6 1 + 2 1 + 3 1 + 4 1 = 1 2 1 9 .
Therefore, a = 1 9 , b = 1 2 , and a + b = 3 1 .