Seven in Four
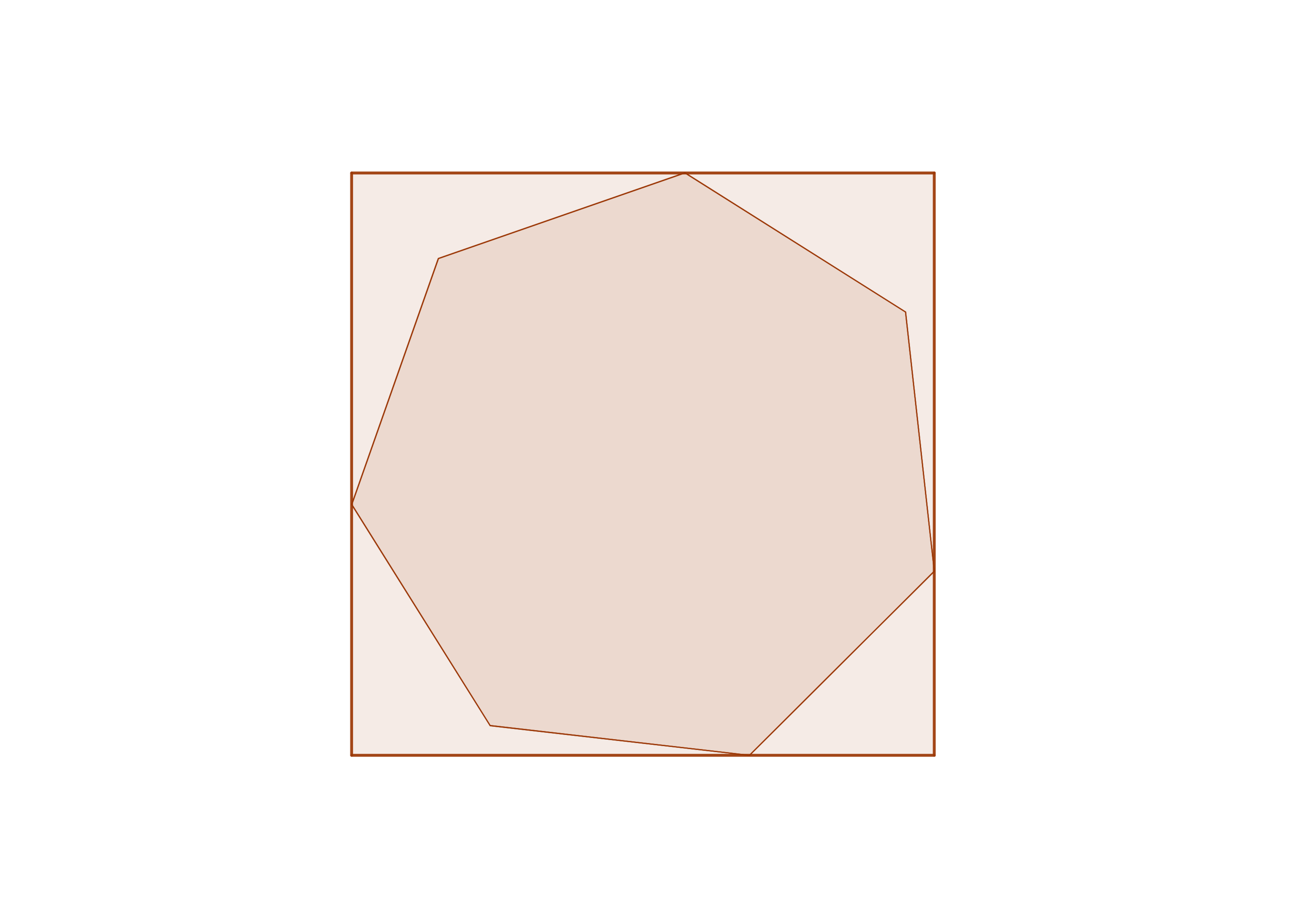
If the area of the maximal regular heptagon which can be inscribed in the unit square is , where and are positive integers, submit .
The answer is 35.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose that p = sin 1 4 1 π = cos 7 3 π . If we put z = e 7 3 π i , then z + z − 1 = 2 p and 0 = z 7 + 1 = ( z + 1 ) ( z 6 − z 5 + z 4 − z 3 + z 2 − z + 1 ) = ( z + 1 ) z 3 [ z 3 + z − 3 − z 2 − z − 2 + z + z − 1 − 1 ] = ( z + 1 ) z 3 [ ( z + z − 1 ) 3 − ( z + z − 1 ) 2 − 2 ( z + z − 1 ) − 1 ] = ( z + 1 ) z 3 ( 8 p 3 − 4 p 2 − 4 p + 1 ) so that 8 p 3 − 4 p 2 − 4 p + 1 = 0 . If we now put t = 2 8 1 π , so that p = sin 2 t , then 4 sin t ( cos 7 t + cos t + sin 5 t ) = 4 sin t cos 7 t + 4 sin t sin 5 t + sin 2 t = 2 ( sin 8 t − sin 6 t ) + 2 ( cos 4 t − cos 6 t ) + 2 sin 2 t = 2 ( − sin 6 t + cos 4 t + sin 2 t ) = 2 ( sin 1 0 t − sin 6 t + sin 2 t ) = 2 [ ( 1 6 p 5 − 2 0 p 3 + 5 p ) − ( 3 p − 4 p 3 ) + p ] = 3 2 p 5 − 3 2 p 3 + 6 p = ( 8 p 3 − 4 p 2 − 4 p + 1 ) ( 4 p 2 + 2 p − 1 ) + 1 = 1 using the fact that 1 4 t = 2 1 π , so that sin 8 t = cos 6 t and cos 4 t = sin 1 0 t , and also using the identities sin 3 u ≡ 3 sin u − 4 sin 3 u and sin 5 u ≡ 1 6 sin 5 u − 2 0 sin 3 u + 5 sin u .