Seven Triangles
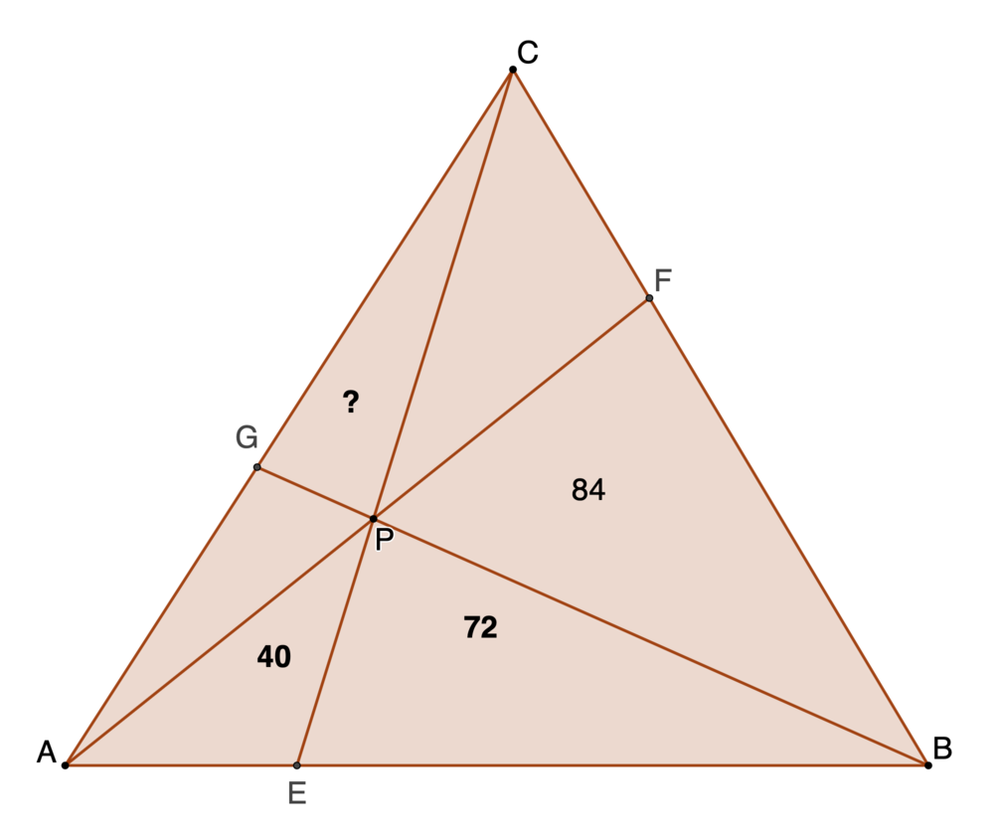
△ A B C has three cevians drawn through P . The areas of △ A E P , △ E P B and △ B P F are 40, 72 and 84, respectively. What is the area of △ G P C ?
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
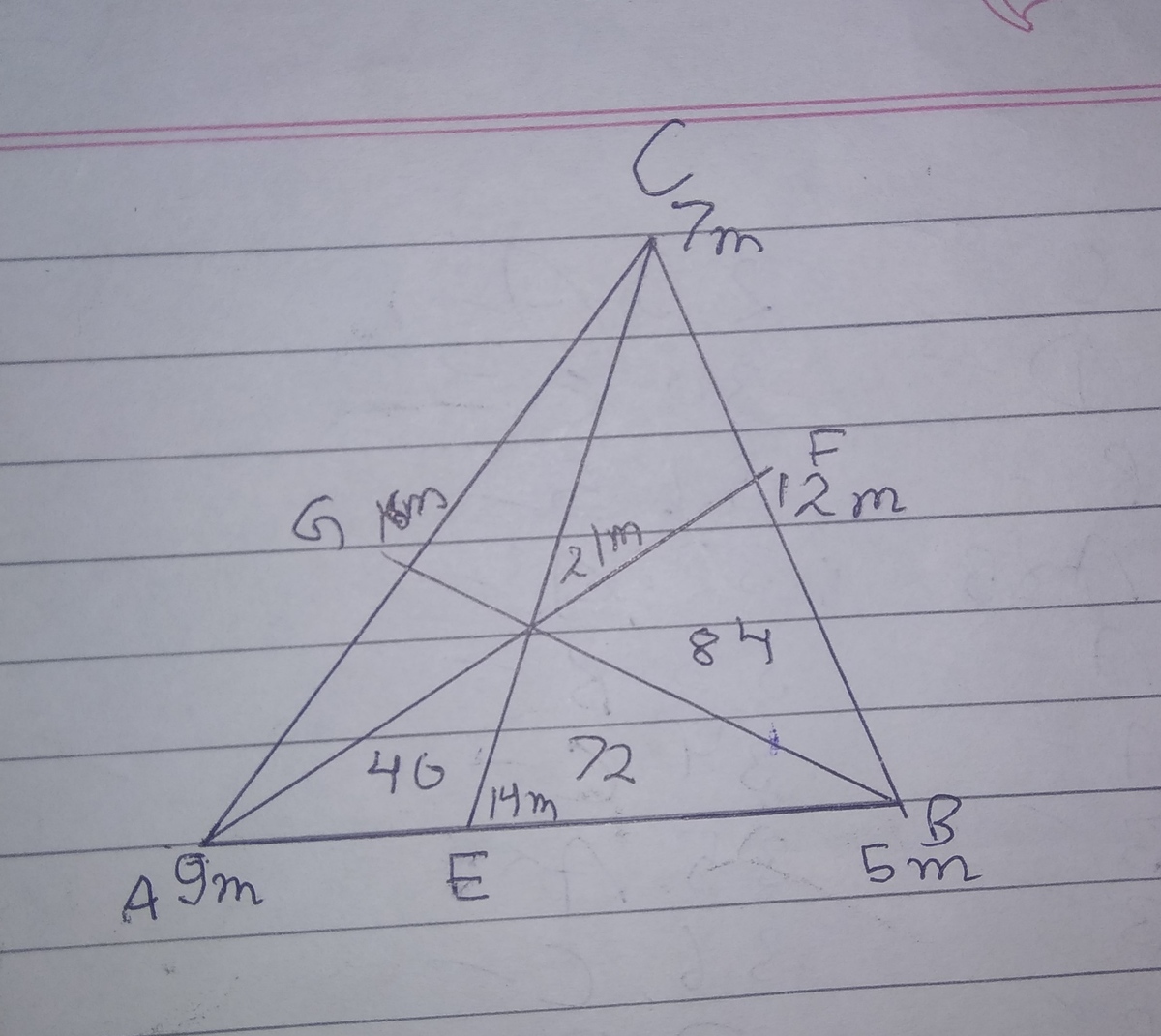
Let's solve using Mass Point Geometry
Now, let's balance A B about E
Now, E B A E = Δ B P E Δ A P E = 7 2 4 0
So, let's keep 9 m mass at A and 5 m mass at B and A B is balanced about E . So, mass at E = 5 m + 9 m = 1 4 m
Let's balance A F about concurrency point P
P F A P = Δ B P F Δ A P B = 8 4 1 1 2
Now, as there is 9 m mass on A , so there is 1 2 m mass at F giving mass at P as 9 m + 1 2 m = 2 1 m .
Now, you can find proof on wiki why all sides will be balanced about respective foot of cevians and all cevians are balanced about P
So, mass at C is 1 2 m − 5 m = 7 m and mass at G is 7 m + 9 m = 1 6 m
Now, as B C is balanced about F , so
( 5 m ) ( Δ B P F ) = ( 7 m ) ( Δ C P F )
5 ( 8 4 ) = 7 ( Δ C P F ) Δ C P F = 6 0
Now, as B G is balanced about P , so
[(5m)(\Delta BPC) = (16m)(\Delta GPC)]
5 ( 1 4 4 ) = 1 6 ( Δ G P C ) Δ G P C = 4 5
Solution may seem long but it is actually very short and time saving while solving.
@Pi Han Goh, I see this type of problem has some interesting history on Brilliant. I was unaware of the Ladder Theorem. My inspiration for the problem came from this paper , which seems to have rediscovered the Ladder Theorem. In the second equation of Theorem 2.1, the author writes:
K 5 = ( K 2 ( K 1 + K 2 ) − K 1 K 3 ) ( K 2 ( K 1 + K 2 + K 3 ) − K 1 K 3 ) K 1 K 2 K 3 2 ( K 1 + K 2 )
or in your nomenclature:
b = ( e ( f + e ) − f d ) ( e ( f + e + d ) − f d ) f e d 2 ( e + f )
But solving the three linear equations you quote from the Ladder Theorem, we get the same equation , with only minor rearrangement of terms. Plugging in d = 8 4 , e = 7 2 , f = 4 0 , we get:
b = ( 7 2 ⋅ ( 4 0 + 7 2 ) − 4 0 ⋅ 8 4 ) ( 7 2 ⋅ ( 4 0 + 7 2 + 8 4 ) − 4 0 ⋅ 8 4 ) 4 0 ⋅ 7 2 ⋅ 8 4 2 ⋅ ( 7 2 + 4 0 ) = 4 5
x is area above y (?) and z below y, solve for y using the following relations
(84)(40)y=(x*z)(72),
84(x+y+z)=(40+72+84)x,
[(40+72+z)/(84+x+y)]=(z/y)
Answer
x=60, z=35
y=45
Let X be the area of △ A G P , Y be the area of △ G P C , and Z be the area of △ C F P :
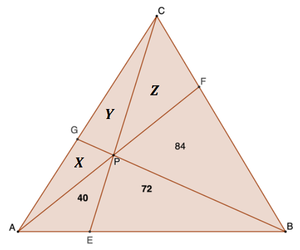
If h 1 is the height of △ A E P and △ E P B and h 2 is the height of △ A E C and △ E C B , then E B A E = 2 1 ⋅ h 1 ⋅ E B 2 1 ⋅ h 1 ⋅ A E = A △ E P B A △ A E P = 7 2 4 0 and E B A E = 2 1 ⋅ h 2 ⋅ E B 2 1 ⋅ h 2 ⋅ A E = A △ E C B A △ A E C = Z + 8 4 + 7 2 X + Y + 4 0 , so that 7 2 4 0 = Z + 8 4 + 7 2 X + Y + 4 0 .
By similar arguments, 8 4 Z = 4 0 + 7 2 + 8 4 X + Y + Z and X Y = X + 4 0 + 7 2 Y + Z + 8 4 .
These three equations solve to X = 3 5 , Z = 6 0 , and Y = 4 5 .
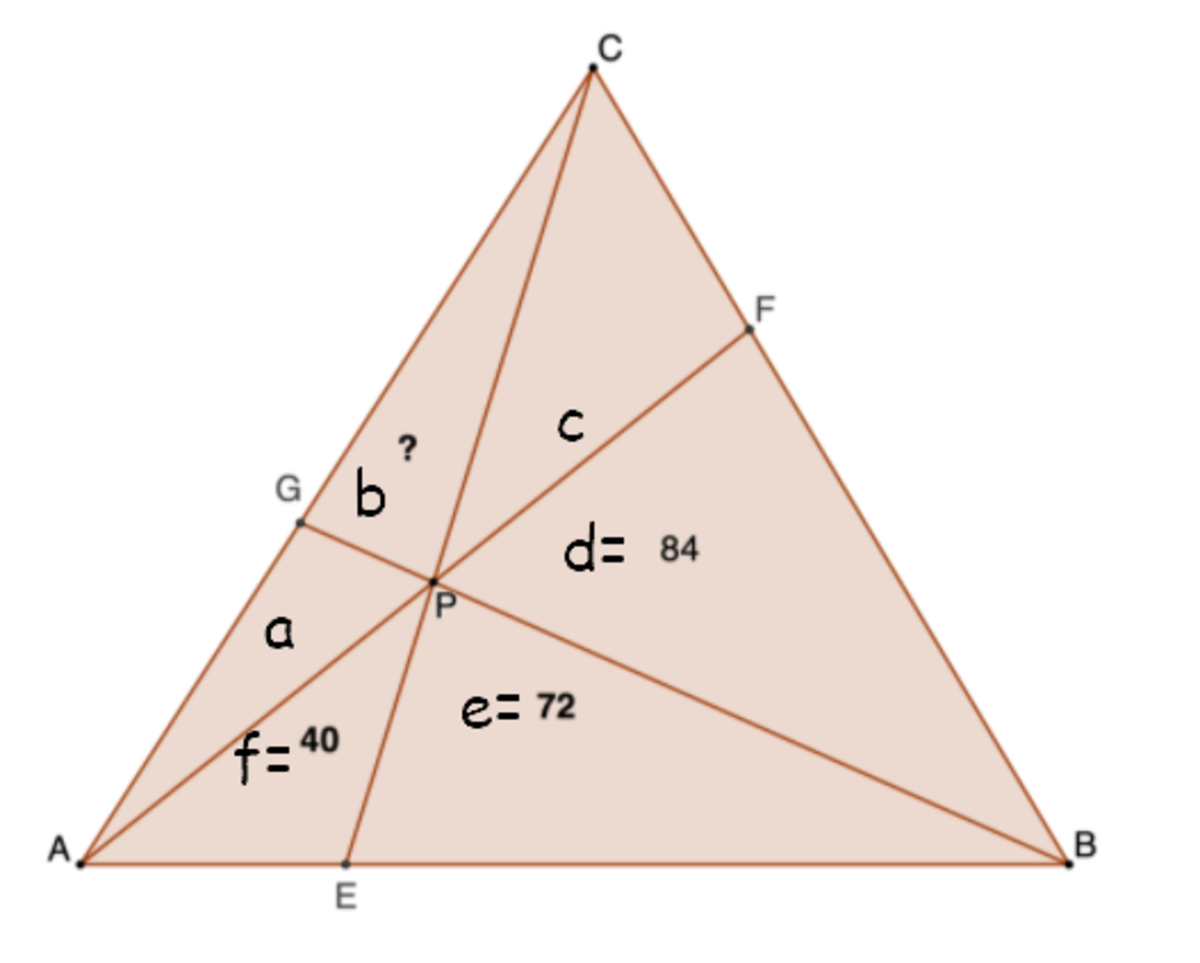
Let
(
a
,
b
,
c
,
d
,
e
,
f
)
denote the areas of these 6 triangles as shown.
 From
Mark Henning's comment under Michale Mendrin's solution
From
Mark Henning's comment under Michale Mendrin's solution
 We are left to solve a system of linear equations,
⎩
⎪
⎨
⎪
⎧
(
a
+
b
)
d
=
(
e
+
f
)
c
(
c
+
d
)
f
=
(
a
+
b
)
e
(
c
+
d
)
a
=
(
e
+
f
)
b
⟹
(
a
,
b
,
c
)
=
(
3
5
,
4
5
,
6
0
)
.
We are left to solve a system of linear equations,
⎩
⎪
⎨
⎪
⎧
(
a
+
b
)
d
=
(
e
+
f
)
c
(
c
+
d
)
f
=
(
a
+
b
)
e
(
c
+
d
)
a
=
(
e
+
f
)
b
⟹
(
a
,
b
,
c
)
=
(
3
5
,
4
5
,
6
0
)
.
Let the areas of △ G P C , △ A P G , and △ C P F be a , b , and c respectively. By Ceva's theorem we have:
G A C G ⋅ E B A E ⋅ F C B F ⟹ b a ⋅ 7 2 4 0 ⋅ c 8 4 = 1 = 1
By Menelaus' theorem ,
G A C G ⋅ B E A B ⋅ P C E P ⟹ b a ⋅ 7 2 1 1 2 ⋅ c + 8 4 7 2 = 1 = 1
Therefore,
7 2 1 1 2 ⋅ c + 8 4 7 2 ⟹ 1 2 c + 8 4 c = 7 2 4 0 ⋅ c 8 4 = 5 c = 6 0
From b a ⋅ 7 2 4 0 ⋅ c 8 4 = 1 ⟹ b = 7 2 4 0 ⋅ 6 0 8 4 a = 9 7 a . Note that the ratio of areas:
[ B C E ] [ A C E ] c + 8 4 + 7 2 a + b + 4 0 9 1 6 a ⟹ a = [ B P E ] [ A P E ] = 7 2 4 0 = 7 2 4 0 ⋅ 2 1 6 − 4 0 = 8 0 = 4 5