Sex-ratio

No matter what conditions you place on stopping having children, the ratio will always be 1:1.

Consider the births as coin flips, and having a girl as flipping heads. You perform an experiment in which you keep on flipping until you flip heads, and then you stop. Then you perform this same experiment many times. Since this process simply involves flipping a coin many times, there will be approximately the same amount of heads as tails. All the experiment does is partition the flips in a certain way.

This is not a mathematical proof, but here is a simple step by step breakdown of this problem that should be more easily accessible to those unfamiliar with mathematical notation.

Imagine you have 1,000,000 couples, all of which have a child.

Assuming that the chances of having a boy or a girl are even (an assumption that really should have been made explicit in the original question) then after all 1,000,000 couples have had their first child, there will be 500,000 girls and 500,000 boys.

The 500,000 couples that had a girl will now stop having children, while the 500,000 that had boys will now try again.

The 500,000 couples trying again will then have, between them, approximately 250,000 girls and 250,000 boys. Add these to the children from the first generation and you now have 750,000 girls and 750,000 boys.

The remaining 250,000 couples with boys now try again, and between them they have 125,000 girls and 125,000 boys. Add these to the children born already and you now have a total of 875,000 girls and 875,000 girls.

There are now 125,000 couples still trying to have a girl, so they try again. Between them, they have 62,500 girls and 62,500 boys. This now gives a total of 937,500 girls and 937,500 boys.

We can see that after every new set of children are born, the numbers still stay evenly split between the total number of boys and girls. This pattern continues without end (theoretically).

Therefore, even though some families will end up with dozens of boys before they get their first girl, the ratio of boys to girls will always remain approximately 1:1.

Consider a specific couple and the expected number of children of each gender they will have. Let $M$ be the expected number of children that are male and $F$ be the expected number of children that are female. The probability that the couple will have $n - 1$ male children followed by a female child is just $\dfrac{1}{2^n},$ since each gender is assumed to be equally likely to occur. Therefore,

$\begin{aligned} F &= \sum_{i = 1}^{\infty} \dfrac{1}{2^n} \\ M &= \sum_{i = 1}^{\infty} \dfrac{n - 1}{2^n}. \end{aligned}$

We can easily calculate $F$ to be $\dfrac{\frac{1}{2}}{1 - \frac{1}{2}} = 1.$ To find $M,$ we first multiply the entire expression by 2 then subtract it from the original expression to make it easier to compute:

$\begin{aligned} M &= \quad \; \; \; \; \dfrac{1}{4} + \dfrac{2}{8} + \dfrac{3}{16} + \cdots \\ 2M &= \dfrac{1}{2} + \dfrac{2}{4} + \dfrac{3}{8} + \dfrac{4}{16} + \cdots \\ 2M - M &= \dfrac{1}{2} + \left ( \dfrac{2}{4} - \dfrac{1}{4} \right ) + \left ( \dfrac{3}{8} - \dfrac{2}{8} \right ) + \left ( \dfrac{4}{16} - \dfrac{3}{16} \right ) + \cdots \\ M &= \dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{8} + \dfrac{1}{16} + \cdots \\ M &= \dfrac{\frac{1}{2}}{1 - \frac{1}{2}} \\ M &= 1. \end{aligned}$

Since $F = M,$ the expected number of children of either gender a couple will have are the same, meaning that the ratio of males to females should be approximately 1:1 after a long time.

We will only consider couples that stopped having babies (meaning they had a girl). For a given couple, the probability to have $n$ children is $\frac{1}{2^n}$ . So the average number of children per couple is $\sum\limits_{i>0} \frac{i}{2^i}$ which is $2$ . As each couple has exactly $1$ girl they will in average also have $1$ boy. This gives us the $50\%-50\%$ sex-ratio.

Consider the viewpoint of the midwife in the hospital. For every mother who comes in about to have a baby, the probability of it being a girl is 50% - it's not affected by the sexes of any previous babies. Every baby being born still has a 50% chance of being a girl so the sex ratio is 1:1.

Let's take a particular couple. We can say that the birth of a girl is considered as a success, while the birth of a boy as a failure. Births are also considered as independent events. Then the number of births required to have a girl, $X$ , follows the geometric distibution with probablity $p=\frac{1}{2}$ . The probability distribution function is $P(X=k)=(1-p)^{k-1}p$ , with mean value $<X>=\frac{1}{p}$ . We conclude that on average, every family in this country is rejoiced to have a daughter after 2 births. Given that the first baby is a boy, after many generations the ratio will be approximately 1:1. We have assumed of course that every family abides by the same birth policy

The explanation is, for example, what @Andrew Hayes says in his post. But here I'm going to prove it practically with help of some code.

$Let \text{ NUMBERCOUPLES} \leftarrow \text{Big enough number}$

$Initialize \text{ male\_child} \leftarrow 0$

$Initialize \text{ female\_child} \leftarrow 0$

$Initialize \text{ i} \leftarrow 0$

$\text{While } i < NUMBERCOUPLES\text{:}$

$\text{----random\_birth} \leftarrow \text{RandomChoice(pos=[0,1], prob=[0.5,0.5])}$

$\text{----if random\_birth equals 0:}$

$\text{--------male\_child++}$

$\text{----if random\_birth equals 1:}$

$\text{--------female\_child++}$

$\text{--------i++}$

A possible output with $NUMBERCOUPLES = 1000000$ could be:

After 1000000 couples there are

Males: 997981

Females: 1000000

Ratio after 1000000 couples: 1.002

Aren't you convinced? Try it for yourself with Python here !

P.S: I've used hyphens (-) instead of spaces because the editor don't let me use more than a few \quad $LaTeX$ commands.

HaHa, easy. I thought about this problem before!! And I know the approximate total number. the total number is double of pregnantable(I cannot sure about the word ㅇㅅㅇ) mother. Just think that half of women pregnant girls and others are boys. Than half of women have to pregnant again and so on. It conclude that if total number of women are n, girls population is 1/2 n+1/4 n+...+1/2 *i n=n(approximate) and boys too.

Others give much more elegant solutions but here's one using limits:

We know that every couple will have exactly one girl, so we want to know the average number of boys that each couple will have. At each birth ${(n+1)}$ there will be ${n}$ boys. Since there is a 50% chance of stopping after each birth we get the probability-weighted sum of

$B = 0*1/2+1*1/4+2*1/8+3*1/16+4*1/32+...$

Which we can write as $B=\sum\limits_{i=0}^n \dfrac{i}{2^{i+1}} = \dfrac{1}{2}\sum\limits_{i=0}^n \dfrac{i}{2^{i}}$

Having the partial sum $S_n = \dfrac{2^{n+1}-n-1}{2^{n+1}}$

By 'many generations' we know we want the limit case, by this we are assuming an undefined number of births from each starting couple or their descendants.

Therefore the expected number of boys $B=\lim_{n\to\infty} \dfrac{2^{n+1}-n-1}{2^{n+1}} = 1$ for each girl

Note that this would assume it were possible for every couple to give birth to enough children to guarantee a girl however if we re-frame the question to consider each branch of the starting family trees and assuming an indefinite number of generations the equations above still describe reality.

A number of children before the first girl (including the girl) is modeled by geometric distribution . Here the probability of success (having a girl) = probability of failure (having a boy, sorry, boys) = $\frac{1}{2}$ = p. The expected value is $\frac{1}{p}$ = $\frac{1}{\frac{1}{2}}$ = 2, practical meaning of this result is "we expect families to have on average two children before the first girl including the girl". Thus, on average, families will have 1 boy and 1 girl which leads to the overall 1:1 balance in the whole population.

A few points: Without any math (and no multiple births) there will always be the same number of females in each generation. “If and only if” means each couple has x number of boys (x includes 0) and 1 girl: 100 couples produce x boys and 100 girls, 277,362 couples produce x boys and 277,362 girls. The number of boys, x, can be greater, less than or equal to the number of couples, but the number of girls will always be the number of couples If there are more boy births than couples(=girls) then in the next coupling there will be the same number of couples as the previous generation and extra boys- who don’t produce offspring If there are fewer boy births than couples (=girls) then there will be fewer couples in the next coupling but there will be equal numbers of boys and girls producing the next generation. This 1 girl- 1 boy for each new couple leads to a 1:1 ratio for the population at large

This of course assumes “old fashioned” coupling rules- not specifically stated in the problem. What if there are excess women and a mother dies after having a girl. Can the father remarry and have additional girls? What about SSM and surrogacy?

One quick way to realize that 1:1 is the case is to imagine the path of a single offspring. For example, A couple has a male and then a female, then stop. The new male goes and finds a female. This couple then has a male and then a female, then stop. Each time the process repeats. Each offspring always goes and finds another opposite gender offspring. So, as the system grows large, the system "equilibrates" to 1:1. 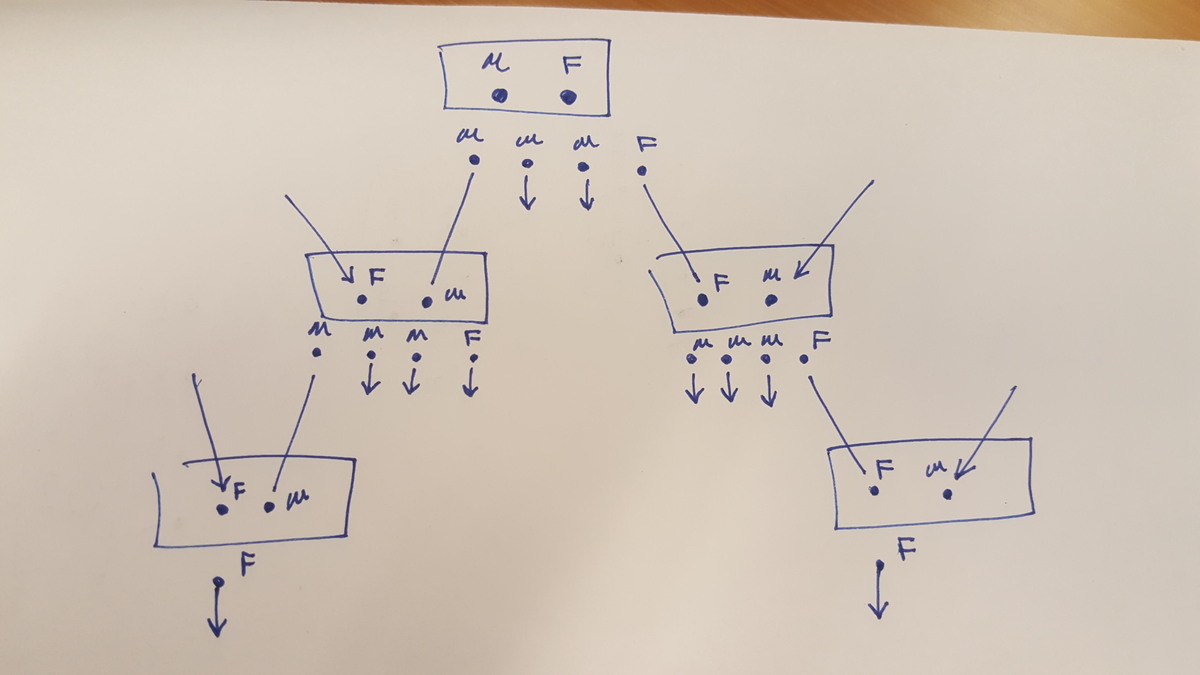*The arrows indicate that these offspring will go and form a couple.

This can be done intuitively. Since excess females will be discarded, every generation will produce equal numbers of males and females, net of the excess.

I am particularly interested in this problem as it goes against our initial intuition, so I would like to try put it in a way that our intuition actually helps us.

Intuitively, we would assume that the couple could have multiple boys and only one girl, thinking that one girl would limit the chance of having anymore, but take note that having a girl also limits the possibility of having any more boys.

for example

B,... B,G BGBGBGBGGBGBGBGBBBBGBBGGBGGGGBGBGGB

correct me if I am wrong but I think it is the law of large numbers that states that the bold part has approximately equal number of boys and girls so technically its a loss for both genders.

( PS its not a proven solution but rather a way to get your intuition to be on your side. )

This solution does of course assume that the probability is memoryless - that whatever a couple's previous history, the chances of a female child will always be 0.5. Imagine a situation where the overall likelihood of a female child was 0.5, but that this masked a variation in likelihoods for individual couples, with, say, some couples having only a 0.3 likelihood and others 0.7. In this situation, selecting out from future breeding those who bear a female child might make a significant difference to the overall gender balance, as the number of children a couple had would be in inverse proportion to the likelihood of those children being female. Effectively this system would be selecting for individuals and couples with a higher likelihood of having male children, which would lead to a population imbalance.

Suppose there are 2^n couples Then no of female children = 2^n because for every couple tha sequence ends with a female No of male children For first child every of 2^n couple have1/2 chance to have boy So we have approx 2^(n-1) boys then for second child from 2^(n-1) there is 1/2 prob to have a boy therefore 2^( n-2) more boys similarly.......... A GP is formed 2^n-1 +2^n-2...........+2+1=2^(n) -1 Therefore ratio is approx 1:1

Half of all kids are girls, so half of all kids are girls. Presuming child gender selection here is a memoryless determination, so the Probabilty P[G] = P[B] for each kid, not matter how many older siblings are in a family, we'll still see gender equality.
The easiest way to see this? Ignore all data at child birth except for the gender of the child.

The weird thing about this nation is that we'll have some families that are extremely large with lots of boys. On the other hand, half of all families will only have one child, a girl.

Assume a bug on the root of a infinite binary tree. Each left child of a node is toxic while each right child is just normal and healthy. The bug chooses repeatedly the next node ( $Pr(\omega_{\text{left}}) = Pr(\omega_{\text{right}}) = 0.5$ ). If the bug enters a toxic leaf, it dies and a new bug is created at the root.

Of course stepping on toxic leafes (without any hidden thoughts) stand for getting a girl, while stepping on green leafes stand for getting a boy. Thus, the height of the tree tells us how many boys were born.

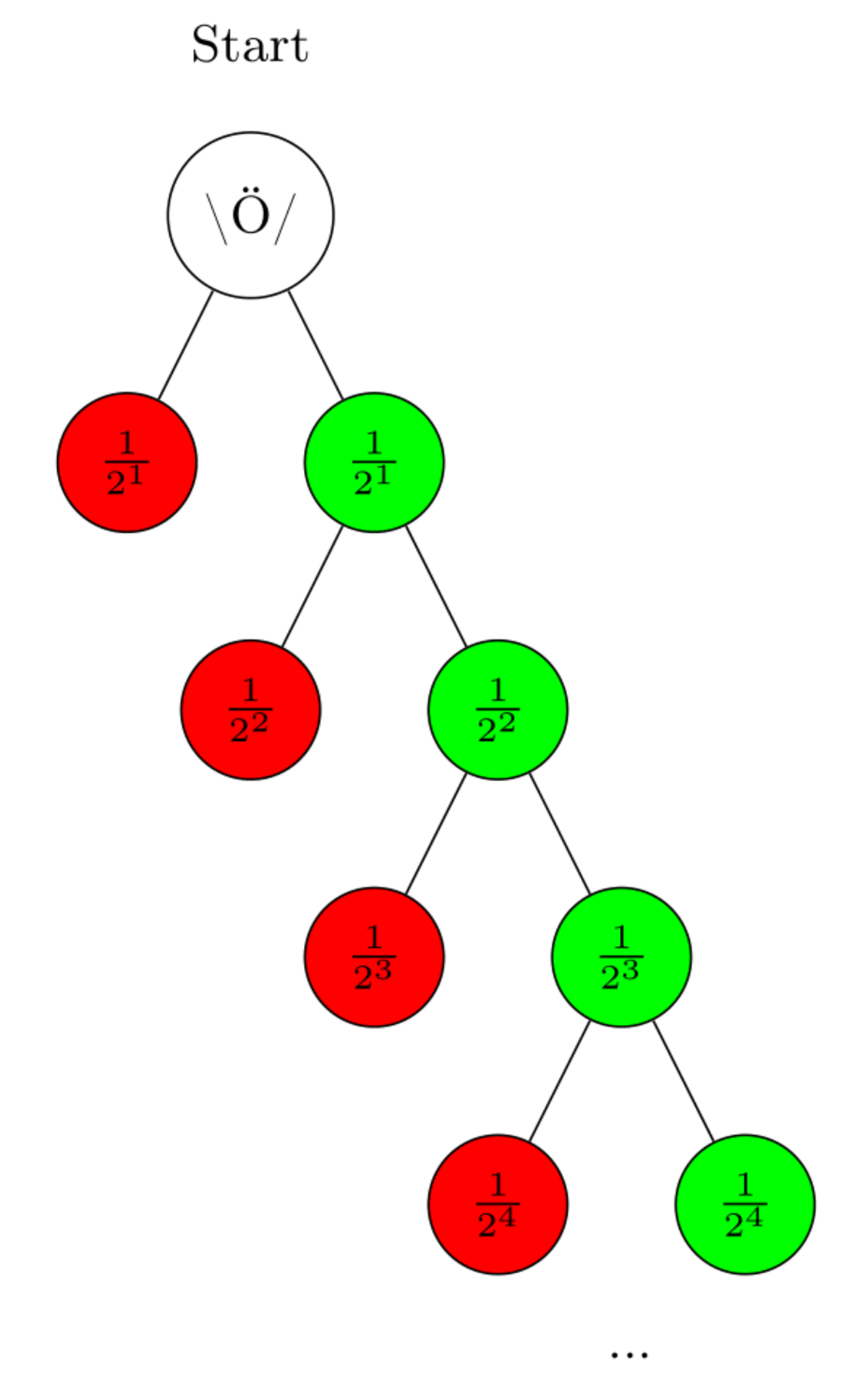
Let's say $X$ is a random variable telling us how far the bug has come. For example, if the bug reaches height $k$ with probability $\frac{1}{2^k}$ (bug chooses every path with probability $0.5$ ), $k-1$ boys were born and of course $1$ girl. We are interested in the mean of $X$ , which equals to the mean of the reached height of all (infinitely many) bugs.

Obviously, $X$ is geometric distributed e.g. $X \sim Geo(p=0.5)$ . This is because we have a chain of bernoulli experiments (left or right with $p=0.5$ ). By looking the mean up or calculating

$E[X] = \sum_{k=1}^\infty Pr(X=k)\cdot k = \sum^\infty_{k=1} \frac{1}{2^k} \cdot k = \sum^\infty_{k=1} \sum^k_{j=1} \frac{1}{2^k}= \sum^\infty_{j=1}\sum^\infty_{k=j}\frac{1}{2^k}= \sum^\infty_{j=1}\frac{1}{2^{j-1}} = \frac{2}{1-2^{-1}} - 2 = \boxed{2}$

we get a mean of $2$ . That is, $2-1=1$ boys and $1$ girl. Thus, the one-girl-regulation will not change the female-to-male ratio in the long run.

PS: In the calculation I used a switching property of positive sums and for the last step the convergence property of the geometric series with $\sum_{k=0}^\infty a_0 q^k = \frac{a_0}{1-q}$ .

PPS: One could also argue evolutionary. See this interesting article about Fishers principle .

The implicit assumption is that children can only be born to monogamous couples, and that those couples keep breeding until they get a girl, at which point they stop. If so, starting with a certain population, the first generation will have a number of children. Every couple will have one girl, while the boys can be in any number. But, even if there are many more boys than girls, a certain number of boys will remain single, and therefore they will not contribute to the process. At the next generations, the process repeats itself. The new couples start having children, they all have one girl and any number of boys. So, the number of girls controls the number of couples, while the exceedance in boys is sentenced to perennial single status.

Hence the expected number of boys for any family is the same as the number of girls. After a long time older generations that did not follow this behavior pass away. With a sufficiently large population, invoking the law of large numbers, the sex ratio will be approximately 1:1.

p.s. In reality, this question would be complicated by the slightly higher rate of male births and the differing risk of death for males and females across lifetimes (females tend to live longer).

The probability of having a male and female is 1:1, therefore no matter where you stop having babies. It will still be 1:1. Probability doesn't change with infinity amount of people.