Shad-ircles
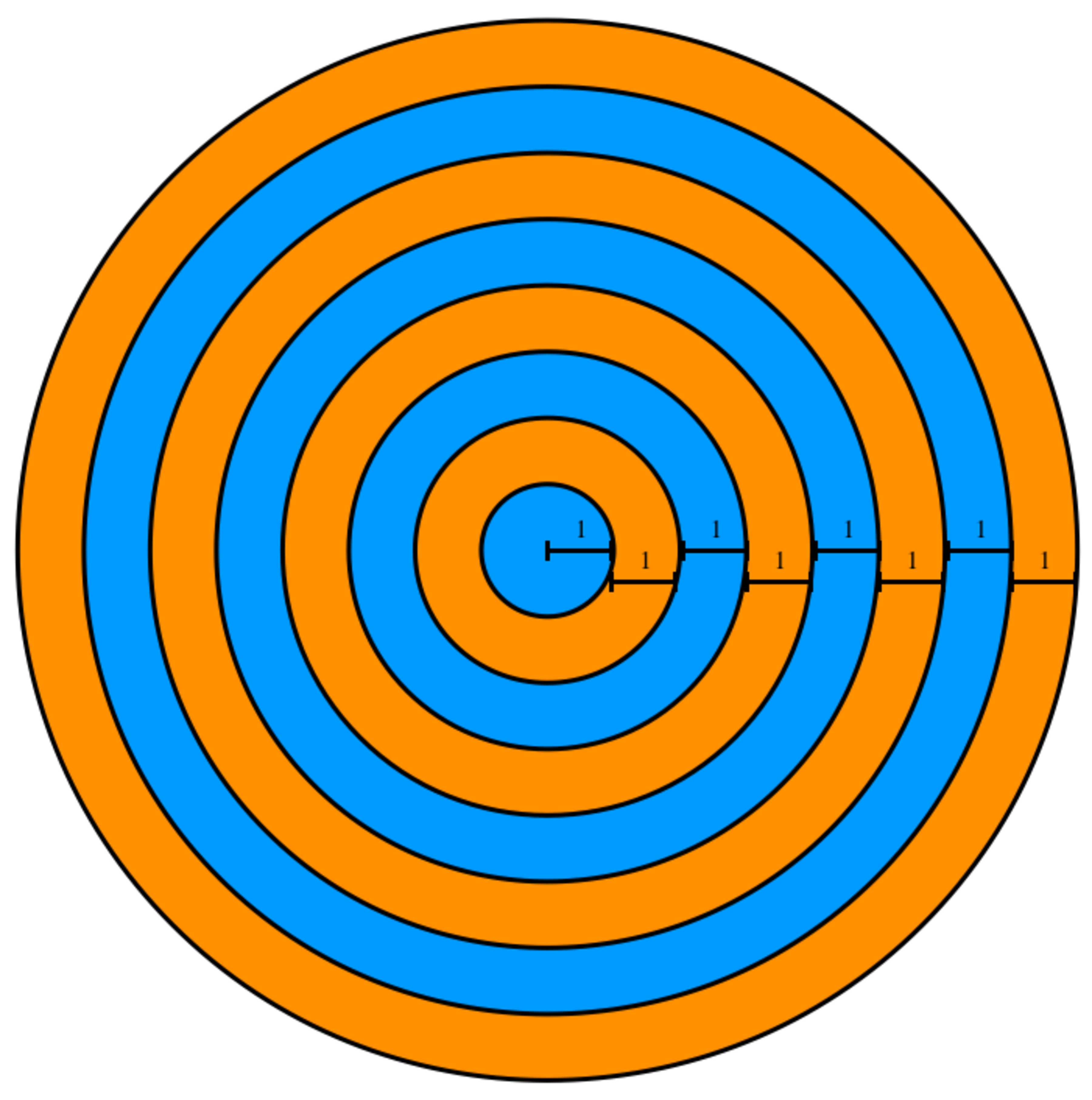
In the diagram, the eight circles are placed at a distance of 1. They have a common centre and have radii of 1 , 2 , 3 , … 8 . What is the ratio of the orange areas to the blue areas?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Easier way my opinion:
sq.: 1 , 4, 9 , 16 , 25 , 36 , 49, 64
Blue area : 1 + (9-4) + (25-16) + (49 - 36) = 28
Red area : 64 - 28 = 36
36:28
9 : 7
Let the areas of blue and orange regions be A b and A o respectively. Then we have:
A b = π ( 1 2 − 2 2 + 3 2 − 4 2 + 5 2 − 6 2 + 7 2 ) = π ( n = 1 ∑ 7 n 2 − 2 n = 1 ∑ 3 ( 2 n ) 2 ) = π ( 6 7 ( 8 ) ( 1 5 ) − 2 × 4 × 6 3 ( 4 ) ( 7 ) ) = 2 8 π
A o = π ( − 1 2 + 2 2 − 3 2 + 4 2 − 5 2 + 6 2 − 7 2 + 8 2 ) = − A b + 8 2 π = − 2 8 π + 6 4 π = 3 6 π
Therefore, A o : A b = 3 6 π : 2 8 π = 9 : 7 .
Great solution especially subtracting A b !
Glad that you like it.
Orange Areas
Sum of Orange Areas = ( π 8 2 − π 7 2 ) + ( π 6 2 − π 5 2 ) + ( π 4 2 − π 3 2 ) + ( π 2 2 − π 1 2 ) = π ( 8 2 − 7 2 + 6 2 − 5 2 + 4 2 − 3 2 + 2 2 − 1 2 ) = π ( 3 6 )
Blue Areas
Sum of Blue Areas = ( π 7 2 − π 6 2 ) + ( π 5 2 − π 4 2 ) + ( π 3 2 − π 2 2 ) + ( π 1 2 ) = π ( 7 2 − 6 2 + 5 2 − 4 2 + 3 2 − 2 2 + 1 2 ) = π ( 2 8 )
OR
Sum of Blue Areas = Area of Bigger circle − Orange Areas = π ( 6 4 ) − π ( 3 6 ) = π ( 2 8 )
∴ Blue Areas Orange Areas = π ( 2 8 ) π ( 3 6 ) = 7 9