Shaded Area
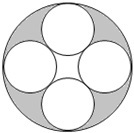 The diagram consists of a large circle and four small circles.
The diagram consists of a large circle and four small circles.
Each of the smaller circles has radius 1 and touches the large circle and the two small circles next on either side of it.
To 3 significant figures, find the value of the shaded area in square units?
The answer is 4.89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
a good method. It can also be solved if we subtract the area of the square plus 4 * (270/360) pi * r^2
The area we need is the area of the larger circle (with radius (1 + sqrt(2)) and the area of the square formed by joining the points of tangency between the 4 smaller circles. Now if we look at the larger circle, we can see that each side of this square forms the hypotenuse of a right triangle with radii ffrom the center of the larger triangle to the points of the tangency. The length of this side = sqrt(2) R where R is the radii of the larger circle which is (1+sqrt(2) as mentioned above. The required area (dark region) = Area of larger circle - Area of square above = pi (1+sqrt(2))^2 - (2+sqrt(2)^2.
Log in to reply
When i mean, points of tangency i mean, points of tangency between the larger circle and each of the smaller circles
Log in to reply
Sorry, i seemed to have missed the point that the line joining the points of tangency (even if it were tangent to the 2 smaller circles ???) would also include portions of the shaded area
gr8!
(y)
very interesting awesome.
excellent
did the same way!!!!!!
I forget the gap at the centre surrounded by the smaller circles, so I get the wrong answer
well explained
pi(root2+1)^2 - 4pi - (4 - pi) = 0.89 (approx)
i did it the same way
how to add pictures in the solution ?
this is what i thought....
the area of un-shade is = 4 x (3/4) x pi + 2 x 2 = 3 pi + 4,
did it the same way, but how can we prove that the quadrilateral created by joining the centers of the four centers of the small circles is a square?
same way!!!
The centers of the four inner circles forms a square of side length 2 . The rest of the area are four three-fourths of circles of radius 1 , so in total that's an area of 3 π + 4 .
The radius of the larger circle is one half of the diagonal of the square ( 2 ) plus 1 . Squaring that, multiplying by π , and subtracting 3 π + 4 yields 4 . 8 8 5 7 … as the answer.
This was way too easy to be a 2200 problem.
Log in to reply
That's why the rating dropped at least 400 in one night!
done in the same way .. :)
Draw the square with its four vertices at the four centers of the 4 small circles. That square has side equal to 2 , so its area is 4 . If you draw the diagonal, the measure is 2 2 . The segment from the center of the big circle to the center of any of the small circles is 2 . Hence, the radii of the big circle is 1 + 2 , and the area of the entire image is ( 3 + 2 2 ) π . The area of the four small circles is 4 π , and the area of the center of the image is 4 − π , because on the square we made there were 4 quarters of the same circle, which is obviously a small circle. Now we subtract...
( 3 + 2 2 ) π − 4 π − ( 4 − π ) = 2 2 π − 4 ≈ 4 . 8 9 .
my exact calculation went up to.... 4.87324547923062......... :O B-p -.-
Step 1:
First * add the centers * of the little circles. It will give a * square and the length of its side is 2 * adding the radius of two circles each having radius of 1.Now we will find the diagonal of the square and that is * 2 sqrt{2}.**
Now,if we see attentively we clearly see that the diagonal of the square+radius of a small circle +radius of a small circle=Diameter of the big circle . Mathmatically it is * 2 * sqrt{2} +1+1 *.If we divide it by 2 we will get the radius of the big circle.
So,the * radius of the big circle is 1+sqrt{2} . So,the area of the big circle is 3.1416 * [1+sqrt{2}]^2=18.31058666. *
Step 2:
Now the intersection area of the square and each small circle is one 3rd of the area of the small circle.So the remaining area of each small circle is 3/4 of its area.
Each small circle has a area of 3.1416 * 1^2=3.1416 and 3/4 of this is 3.1416 * [3/4].
There are four small circles. * So we have to multiply this by 4 which results in 3 * 3.1416. *
The area of the square is 4.
So, the area covered by the square and small circles is 4+3 * 3.1416.
Now we have to substract this from the area of the big circle to get the area of the shaded area.
So, 18.31058666-3 * 3.1416-4=4.89
This is our desired area and the answer is 4.89
At first draw straight lines from centre of each small circles to make a square of side 2 units(within the bigger circle). Calculate the diagonal of the square formed using formula (2)^1/2 * a (sorry i don't have the root sign ) then extend the diagonal so that it touches the bigger circle . So we get radius of the bigger circle which is 2.414 units. Now the area of the square is 4 sq.units and the net area of small circles is 3 pi 1 sq units. Now add this area to square's area and subtract it from the area of the bigger circle's area i.e.(18.3105 - 13.4247)=4.8858 = 4.89 .
Dude give solution not answer!
- Construct a square by joining the centers of 4 small circles. Diagonal of square = 2 sqrt(2) and Diameter of large circle = Diagonal of square + 2 radius of small circle = 4.828
- Using step 1, Calculate area of large circle and subtract area of square and area of 3/4s of 4 small circles to get the area of shaded portion.
 alt text
alt text
Let the radius of the smaller circles be
r
.
Let the radius of the larger circle be
R
From the figure, clearly,
2 R = 2 r + ( 2 r ) 2 + ( 2 r ) 2 = 2 r ( 2 + 1 )
R = ( 2 + 1 ) r
Now,
Area of the unshaded region
=
Area of square formed by joining the centers of the circles
+
4
(
4
3
)
π
r
2
Area of the unshaded region
=
4
r
2
+
3
π
r
2
Hence,
Area of the shaded region
=
π
R
2
−
Area of the unshaded region
Area of the shaded region = 4 . 8 9 s q . u n i t s
It is asked to find upto 3 significant fig. so it should be 4.885
Log in to reply
4.885 is 4 significant figure.... so ans is 4.89(after rounding off )
As you can see, radius of the bigger circle is 2 + 1
Area of bigger circle= π ( 2 + 1 ) 2
Area of 4 smaller circles= 4 × π ( 1 ) 2 = 4 π
Area of the gap at the centre surrounded by the smaller circles = (Area of square ABCD) - (Area of the four quarters of smaller circles centred at A, B, C and D)
= 2 2 − 4 × 4 1 π ( 1 ) 2 = 4 − π
So, the area of shaded region= (Area of bigger circle) - (Area of 4 smaller circles) - (Area of the gap) = π ( 2 + 1 ) 2 − 4 π − ( 4 − π ) = 4 . 8 9 (approx.)