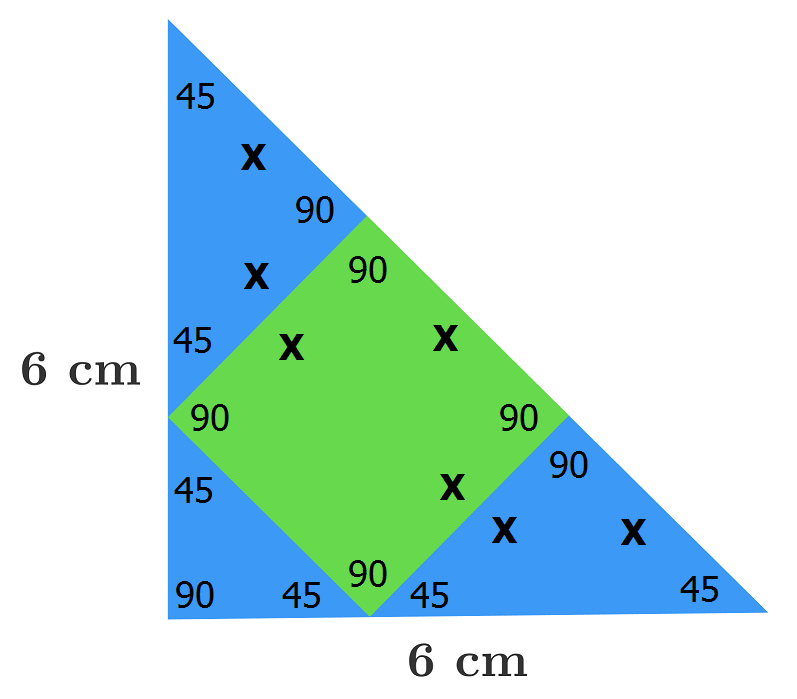
Square In Right Triangle
 Find the area (in
cm
2
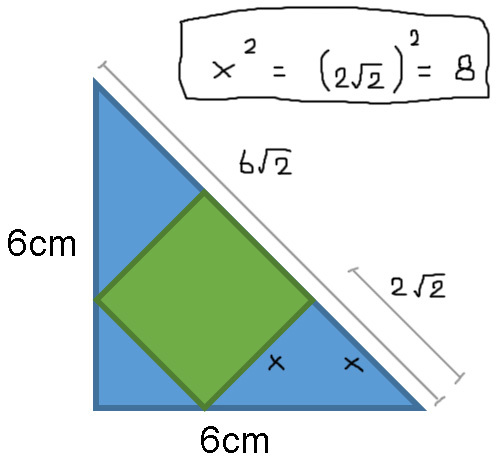
) of the shaded green square in the blue isosceles right triangle, whose legs have length 6 cm.
Find the area (in
cm
2
) of the shaded green square in the blue isosceles right triangle, whose legs have length 6 cm.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
49 solutions
Your answer is the simplest
im too stupid :( how could i not see that
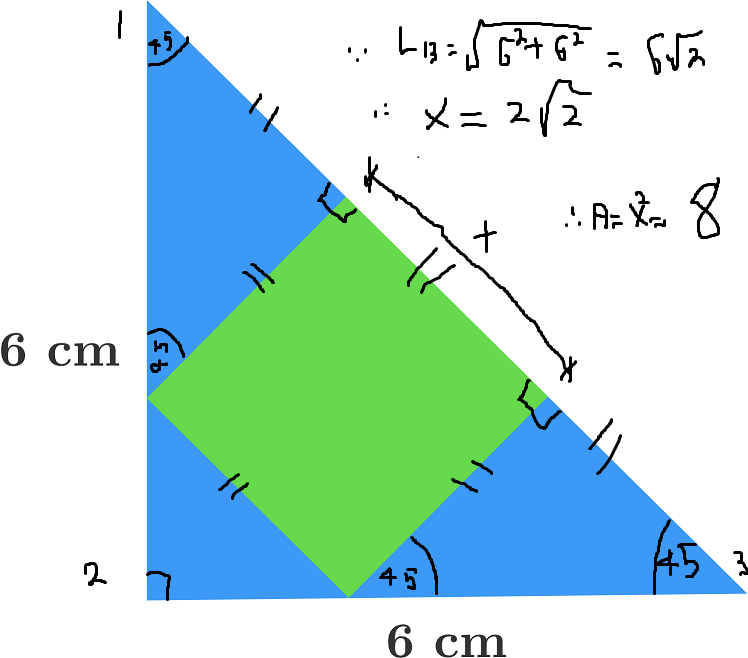
First you should proof that: all these triangles are congruent
Log in to reply
Since triangles 7 and 6 are both isosceles right triangles with a shared hypotenuse, we know they must be congruent. We can use this to show that all other triangles are congruent.
Same way ( ͡° ͜ʖ ͡°)
Such an elegantly simple solution!
I think @mongol genius has a point. I also realised that this triangle looked like it's made up by 9 smaller pieces, but I couldn't prove it mathematically.
True. Very good. It should be noted that the graphic is deceiving because on the original problem, the triangles are not drawn accurately. However, it is mentioned that there is a green square, making all sides equal length.
Each small blue triangles are 4 5 − 4 5 − 9 0 . Also, the big hypotenuse is 6 2 . That hypotenuse is being divided in three equal segments of length 2 2 , because the two blue segments are part of each 4 5 − 4 5 − 9 0 triangles, and hence they're equal to the side of the square. by that way we find the area of those two triangles: 2 2 2 ⋅ 2 2 = 4 each one. We know those two triangles are exactly two halfs of the green square because they share the sides lengths. Finally, the area of the green square is 4 ⋅ 2 = 8 .
Good solution, same way I did it. But just to make it easier, you can just square the side length of the square to find its area rather then add the areas of the 45-45-90 triangles.
Hey, how did you find the hypotenuse is being divided into three equal parts?
Log in to reply
That's a fair assumption that you can make from the diagram.
Log in to reply
Though that's the way I did it, why is it a fair assumption that it's divided into three parts? My reasoning was that since it was a square within a "half-square" (so-to-speak), it was likely that the hypotenuse was divided into 3. But that's such flimsy basis to me...
I think its like this, since the corner blue triangles are 45-45-90 triangles, two of their sides must be equal. Therefore the side of the square is equal to the blue side.
A good way to think of this problem is to break it down into various pieces in order to avoid making any unfounded assumptions.
The first thing to notice is the fact that this is an isosceles right triangle, because (1) the problem specifies that it is right, and (2) both of the legs are 6 cm, thus arriving at the definition of an isosceles right triangle. But how does this help us?
Well, by taking points [1] and [2] into consideration, we know that (3) the top and rightmost angles of the big triangle both measure 45 degrees. This is because the angles of a triangle add up to 180 degrees, and because one angle is 90 degrees and the remaining two are equal, they must be 45 degrees each. Let's keep this in mind for a future step.
What else can we work with? Well, we also know that the angles of a square form 90 degree angles. By using this in conjunction with the fact that straight lines measure 180 degrees, we know that (4) the angles of the smaller two triangles that lie along the hypotenuse of the larger triangle are both 90 degrees as well.
Because [3] states that the top angle of the top triangle is 45 degrees, and [4] states that the right angle of the top triangle is 90 degrees, we know that (5) the remaining angle of that triangle is 45 degrees as well (since a triangle's angles must add to 180 degrees). We can follow the same argument for the triangle on the bottom right.
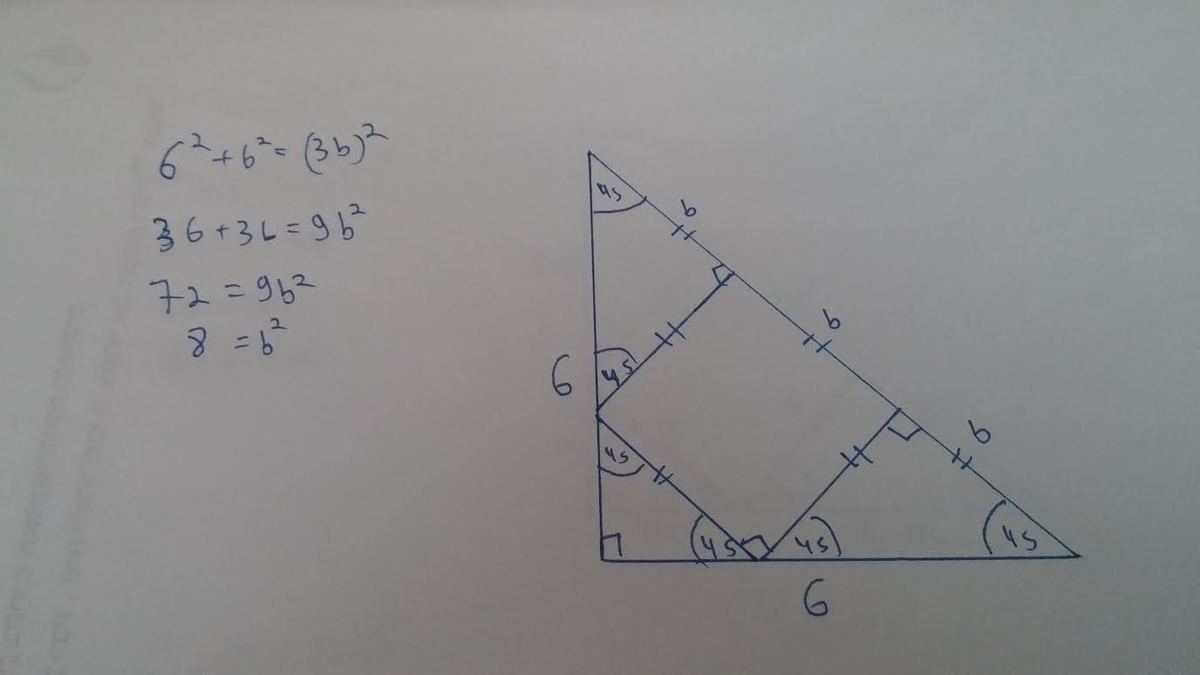
By using points [3] and [5], we deduce that the smaller triangle on top and on the right are isosceles as well, since two angles measure 45 degrees. By using the definition of isosceles triangles, we know that the length of any side of the square (let's call it "x") is the same as the length of the smaller triangle side along the hypotenuse. Thus, because the top triangle contributes a length of "x" to the hypotenuse, the square side contributes a length of "x" to the hypotenuse, and the bottom right triangle also contributes a length of "x" to the hypotenuse, we can conclude that (6) the hypotenuse is of length "3x".
Finally, by applying the Pythagorean Theorem, we find that the length of the hypotenuse squared should be 36 + 36, or 72. Thus, (7) the length of the hypotenuse is the square root of 72. Using points [6] and [7], we can then set this up as:
3 x = 7 2
and by simplifying the square root of 72, we get
3 x = 6 2
dividing 3 off both sides, we get
x = 2 2
where "x" measures a side of the square.
To find the area of the square, we must square the side length, or "x".
Area = x 2
Recall that x = 2 2
Area = x 2 = ( 2 2 ) 2
Area = ( 2 2 ) 2
Area = 2 2 ∗ 2 2
Area = 4 ∗ 2
Area = 8
Q.E.D.
superb explanation .
Best explanation on this thread.
The most logical and assumption free explanation.
Crystal clear
Same, and very detailed!
This is both mathematically sound and simple to follow. Good job
The best way to solve the problem!! Indeed it is necessary to assume that the side of the square is exactly 3 times smaller than the hipo...
if the side of small blue triangle is x, then the side of the green square is 2 x 2 , so 2 1 6 2 = 2 1 x 2 + 2 x 2 + 2 x 2 , x = 2. So green box is 8.
The shortest way and a very clear solution
We get total area is 18 cm2. Assume we can divided 9 same areas from this triangle. Then we get green areas is 4/9 from this triangles. so green areas=(4/9)18= 8 cm2
yea correct!
I like your solution
Because the big triangle is isosceles right triangle so two small right triangles of both sides are isosceles ones. Therefore, [the side of the square] = 1/3 [hypotenuse]. Eventually, [area of the square] = 1/9 [hypotenuse squared]= 8.
An easy and intuitive way: drop down a vertical line that divides the green region into two triangles: A and B, where A is the one to the left, and B to the right. A and B are congruent because of common side ( the vertical ) , right angle, and alternate angles. A shares a common side with the top blue triangle, and also has the same interior angles, from the alternate angle rule. So A is congruent to the top blue triangular area by side-angle-side rule. Similarly, B is congruent to the bottom right area. Now, as for the bottom left blue triangular area, you can see that, if you split A further into two, one of the halves are congruent to the bottom left triangular area; again, they have common side and two equal interior angles. So the bottom left triangular area is congruent to half of A. So basically, the total area 18 = top left blue triangle + bottom right blue triangle + A + B + bottom left blue triangle = A + A + A + A + (1/2 A) { since A is congruent to top left blue triangle, B to the bottom right blue one, A to B, and the bottom left blue triangle to half of A }; therefore, 18= 4.5A, which implies A = 4, or, 2A= green area equals 8.
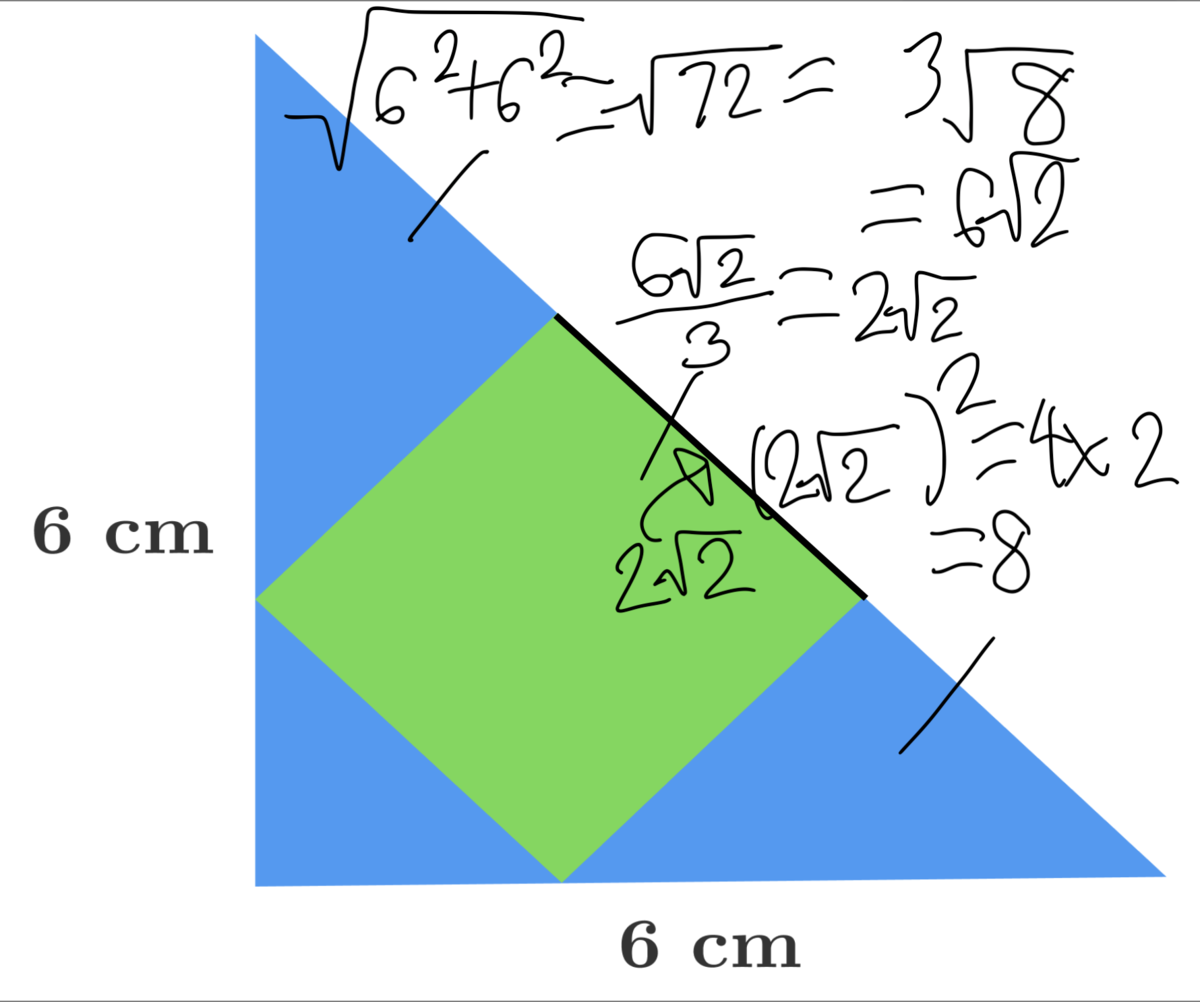
According to Pythagorean theorem the hypotenuse to the triangle will be 6√2 and can be divided into three equal parts resulting in 2√2 cm each which by means is also the side length of the square inscribed in the triangle! Area of square=a²=(2√2)²=8cm.
Draw the diagonals of the square, suppose each has length 'd'. Now with a minimal effort it can be shown that each of them are parallel to one of the '6 cm' sides. In that diagram, with a trivial deduction, it becomes obvious that each of the corners of the square that don't lie on the hypotenuse, cut their respective 6 cm sides 'd/2 cm' above or beside the vertex opposite to the hypotenuse. Now consider one of the minor triangles with 'd' as base and having a common vertex with the larger triangle and compare it with the larger triangle (i.e. the triangle in the figure). they are 'similar'. So, comparing their sides, (6 - d/2)/6 = d/6 => d=4, area of the square = d^2/2=8
If x is the hypotenuse of one of the two small identical right isoceles triangles, then the length of one side of the square is x/sqrt(2) since the two idenntical smaller angles of the smaller triangles are each 45 degrees. Thus (3x/sqrt(2))^2 = 2*6^2, x=4 and the square's area is (4/sqrt(2))^2 or 8 cm^2.
This is an isosceles right triangle, so the sides of such triangle are x:x:x√ (2) Thus, the hypotenuse is going to be 6√ 2 / 3 = 2√ 2 -Divide by 3 because this side is partitioned into 3 equal parts Area of square is s * s = 2√ 2 * 2√ 2 = 8
The triangles are 45 45 90 triangles. Let the length of the box be c. csqrt2 + c/sqrt2 = 6. c=2sqrt2, c^2=8
We can see that the point where the square touches the legs of the triangle divides each leg into two parts. Let the larger of these parts have a length of a . Therefore, the smaller part is 6 − a .Let the side of the square be S .
Now, it can be proved that the two large blue triangles (the ones touching the hypotenuse) formed on either side of the square are congruent and isosceles right triangles. (by AAS criterion) ⇒ 2 a = S .
Similarly, the smaller blue triangle (the one not touching the hypotenuse) is also isosceles and right angled.
⇒ ( 6 − a ) ⋅ 2 = S .
Therefore, 2 a = ( 6 − a ) ⋅ 2 ⇒ a = 4 .
⇒ S = 2 4 = 2 2 .
So, the area of the green square = ( 2 2 ) 2 = 8 c m 2
Quod Erat Demonstrandum (QED).
By using the Pythagorean Theorem to find the hypotenuse: /(a^2)
The problem can be solved once we realise that the all the 3 blue triangles are similar to the bigger triangle after which we can realise that the vertex of the square divides the bigger triangle in the ratio of 1:2. Now the side of the square can be calculated by pythagoras theorem. And you can calculate the area of the square as 8 units.
Since the legs are 6 cm each, the hypotenuse of the triangle would be √6²+6²=6√2. We can see that one side of the square is easily 1/3rd of the hypotenuse, making its' length 6√2 / 3, or 2√2. Then, the area of the square is (2√2)²=4 x 2=8 ☺☺☺☺
I made it simple. First I guessed that the smallest length of the smallest triangle is half of the lenth of hypothenuse of the bigger triangles, so 2 cm. Then I used the pythagore theorem, 2^2 x 2^2 = 8
Area of bug triangle 6×6×1/2 = 18 One side is 6cm From pic it is clear that 1 side is equal to diagonal of a square(imaginary) and half diagonal of next square so length of square diagonal 6/1.5= 4cm So, by Pythagorean Theorem If side of square is x then x² + x² = 4² x² = 8 come So 8cm² is the area of square
Assuming the large triangle is a right triangle: Both sides of the triangle being 6cm tells us it is a 45-45-90. We can combine this with the knowledge that the green figure is a square (90-90-90-90).
 This proves that the smaller blue triangles are also isosceles.
If the green square has side length X, the two smaller 45-45-90 triangles must also have sides length X.
This makes the total length of the hypotenuse = 3x = 6√2
Thus x = 2√2 and x^2 = 8
This proves that the smaller blue triangles are also isosceles.
If the green square has side length X, the two smaller 45-45-90 triangles must also have sides length X.
This makes the total length of the hypotenuse = 3x = 6√2
Thus x = 2√2 and x^2 = 8
You could also say that because the three opposing triangles are 4 9 of the square's area (due to the two large ones equaling the square in area plus one quarter of the square for the smaller one), the area of the triangle is 9 4 of the area, which is simply 8
Use Pythagoras to determine C (long side of triangle.)
Divide by 3 for length of square.
Square for solution.
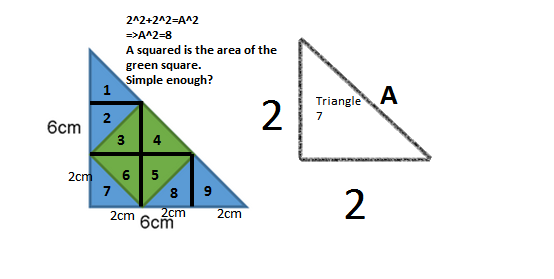
If you don't know the area of the right triangle, this can be another solution. @Nano Noor , I hope you won't be mad at me!
The diagonal of the square is parallel to one of the sides. Therefore the following proportion: d/6=6-(d/2)/6 which implies that d=4. Area=d**2/2.
The area of the square is 9 4 part of the triangle
Hypotenuse is length \sqrt{6^{2) + 6^{2}} =\sqrt{72} Side if square is 1/3 of hypotenuse i.e. \sqrt{72}/3 Area of square is \sqrt{72}/3^{2) = 72/9 = 8.
The one side of the square is 1/3 the length of the hypotenuse, so if you use Pythagorean theorem to find the length of the hypotenuse, and then divide by three and square, you get the answer. Ex: 6^2+6^2=72, sqr rt 72=8.5....., 8.5...../3=2.8......, 2.8.....^2=8
This is a right angled isoscles triangle so angles are 90,45,45 now by applying sine and cosine values we can know that the sides other than hypotenuse are divided into 2:1 i.e., 2cm aand 4 cm now look at triangle on left corner its hypotenuse is sqrt(2^2+2^2)=2√2 so area of square is 2√2*2√2=8
Hyp=\sqrt{72} Side = hyp/3 Area=S^{2}=approximately7.8=8
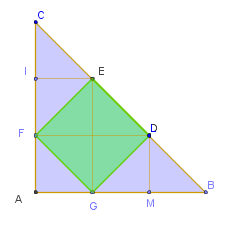 – The square meets both sides such that all blue right triangles are isosceles. Hence side of square is 1/3 of hypotenuse H
H = sqrt(6^2 + 6^2) = 6
root(2)
Hence side of triangle = 2
sqrt(2) and Area of square = 8 cm^2
The Triangle may be divided in 9 small right triangles. All these are equal in area. Hence area of square = 4 * area of large triangle / 9 = 4 * (6
6)/(2
9) = 8 cm^2
– The square meets both sides such that all blue right triangles are isosceles. Hence side of square is 1/3 of hypotenuse H
H = sqrt(6^2 + 6^2) = 6
root(2)
Hence side of triangle = 2
sqrt(2) and Area of square = 8 cm^2
The Triangle may be divided in 9 small right triangles. All these are equal in area. Hence area of square = 4 * area of large triangle / 9 = 4 * (6
6)/(2
9) = 8 cm^2
technicly you have to prove that triangles CIE EDO, and DMB are equal and then you can say ED is one third of hypotenuse
You should realize that the triangles obtained are isoceles. Then, if you understand what it implies, the sides of the square have the same lenght of the non-hypotenuse sides of the triangles, since the length of the hypotenuse of the big triangle is known (by Pythagoras) then the lenght of the sides mentioned are the lenght of the big hypotenuse divided by 3.
right triangle and two equal sides imply that the other two degrees are both 45. now comes a little imagination, first we know that a square can be divide into triangles and we can see that the smallest triangle in this picture is the bottom left one, so if we divide the other parts with it we get top left triangle = bottom right triangle = 2 smallest triangle and green square = 4 smallest triangle. this gives us 1+2+2+4 = 9 smallest triangles. since square = 4 triangles, we know immediately its area is 4/9 of the total area which is 6x6/2 = 18 so we got 18x4/9 = 8
This is the right triangle. So use Pythagorean Theorem we have the longest side is the square root of 36 + 36 = 72. So the hypotenuse's length is 6√2. The hypotenuse is divided into 3 equal part so 3x= 6√2 => x = 2√2. Finally the area of the green square is 2√2 *2√2 = 8 (cm^2)
Going for simple here:
As it is, by definition, an Isosceles triangle (two adjacent sides equal in length), we can say that putting a square (note: not a rectangle) with vertexes touching those equal sides, the hypotenuse of this right triangle will be divided in 3 by the edge of the square.
Using the Pythagorean Theorem, we know that the hypotenuse is 7 2 , so, as we want to find the length of the square's edge, we divide the hypotenuse by 3. Edge = 3 7 2 .
To find the area of the square:
( 3 7 2 ) 2 = 8
the center of gravity of the triangle is also the center of gravity of the square, which is 1/3 of the height or base. therefore the diagonal of the square is equal to 2 x1/3(6) = 4. Hence the sides of the square(x) can be computed as x^2 + x^2 = 16: x=8^.5.the area therefore is x^2 = 8 sq.cm
By observation, look that the green square area is egual to 4 times the area of little blue triangle in botton left. The b and h of this little triangle are 2, so his area is b*h/2 = 2. Then square area is 4 * 2 = 8!!!
Forgotten hypotenuses, forgotten square roots!!!
Blue triangle on either side of square equals 1/2 it's area, small triangle is 1/4 of square. If we name square x, than the total area of triangle = 2.25x. Area of triangle is 1/2b*h. Area of triangle is 18. 2.25x=18. x=8
first, solve the hyp or hypotenuse (X),; X= 6^2 +6^2 = the square root of 72; focus on the hypotenuse... who will notice or by inspection the length of two blue lines is equal. so, yo may let y = one blue line in the hyp. then let z=the green line in the hyp. . So, y+z+y= the square root of 72; or 2y+ z = the square root 72; (eqtn 1) by inspection again; the small triangle formed in the lower right side is an equilateral triangle, in which we can say that the side of the square of the green line in the hyp is just equal to the blue line in the hyp. or y=z --> substitute to eqtn 1 2y+z = the square root of 72 2y + y = the square root of 72; 3y = the square root of 72; y= 2 X the square root of 2
Area of the square is equal to the square of y. A= the square of ( 2 X the square root of 2) A= 8 cm^2
i hope my solution helps.
benedictoamorajr
The two larger blue triangles are each half of the area of the green square. The smaller blue triangle is a quarter the area of the green square. Thus the blue region is 2(1/2)+1/4 = 5/4 times the area of the green square. Therefore the area of the green square is 4/(4+5) = 4/9 times the area of the largest triangle, which is 6 6/2 = 18. Hence the area of the green square is (4/9) 18 = 8 cm^2.
consider ABC as big right angled triangle and side of the square present on hypotenuse be PQ and R be the point on AC side of the triangle and S be on AB then now let RC be x cm and AR be y cm it => x+y = 6 let it be equation 1 from triangle QRC sin (QCR) =sin 45 = QR/RC = 1/square root of 2 it implies QR =x/square root of 2 there fore side of a square is x/square root of 2 let it be equation 2
now similarly as we consider for the triangle ARS cos ARS =cos 45= AR/RS=1/ROOT OF 2 =>RS=y ROOT 2 which is also a side of a square there fore y *ROOT 2 =x/square root of 2 => x=2y from eqn 1 3y = 6 and => y = 2 => x = 4 area of square = x/square root of 2 *x/square root of 2 =x square / 2 = 4 4/2= 8
Since both sides of the large blue triangle are equal, the angles opposite the 90 degree angle are both 45 degrees. By definition of a square, the angles in the green square are all 90 degrees, so the angles formed by the square with the hypotenuse of the large blue triangle are 90 degrees. Thus, the smaller blue triangles formed with the hypotenuse are isosceles right triangles -- with the sides formed by the right angle being equal to the side of the square. This is why the hypotenuse of the large blue triangle is divided equally into 3 parts. Since 6^2+6^2 = hypotenuse^2, the hypotenuse = squareroot(72) = 6 squareroot(2). 1/3 * 6 * squareroot(2) - 2 * squareroot(2) = side of the green square. Area of the square = (2 squareroot(2))^2 = 8.
2 x 9 = 18 => 2 x 4 = 8 {Ultimate}
[1/3 x 6 Sqrt(2)]^2 = 8 {Direct}
Solving y^2 + x y + (1/4) x^2 = 18 and x = y => x^2 = 8 {General}
The third shall be the most convincing. Sqrt(2) from Pythagoras' Theorem for square of side length of 1 should be a known to people who attempt to solve.
No. Here, 9 is derived from 1 + 2 + 2 + 4. You fold blue onto green and fold the green square twice again into a unit triangle of which 4 of them make the green square. A unit triangle is 2 cm^2. Green: 2 x 4 = 8 and Blue: 2 x 5 = 10. Total area = 18 cm^2.
9 is derived from the formula: Area of square = s2 there 3 x3..do you agree?
as right triangle (Isosceles) hypotenuse is equal to 6 square root 2 then the side of the square = 1\3 the hypotenuse then we can find the area = (2square root 2)^2
area of triangle is 1/2 * 6*6= 18 also area = 1/2 *6 root (2) * perpendicular hence perpendicular length = 3 root 2 . let side length be x for square. then (3 root 2 - x)/x= 3 root 2/6 root 2 which gives x = 2 root 2. hence area = 8
My solution can solve this problem without knowledge of square root.
We easily calculate that the area of triangle 6 * 6 / 2 = 18
Now suppose we draw two lines which each line connect two opposite point of green square, we have four triangle. Each triangle has area S
We easily probe that the are of top triangle equals 2S, triangle in the left has area S, and triangle in the right has area a 2S
Now we have: (2S) + (4S) + (S) + (2S) = 18, therefore S = 2
The area of square equals 4S = 8
Hypotenuse is:
sqrt((6 6+(6 6))=6*sqrt(2)
the length of the square is:
Hypotenuse/3 = 2 * sqrt(2)
so area of square is : (Hypotenuse/3 ) (Hypotenuse/3) = (2 * sqrt(2)) (2 * sqrt(2)) = 8
Even though the answer arrived at by Mr. Rakib is correct, he did not get his first equation right. The hypotenuse is Sq.root of (36+36)=3*Sq.rt (8) . Therefore one third of the Hypo. is a side of the sqare, which is Sq.rt.(8). Therefore the area of square is 8sq.cms