Shadow Blocks
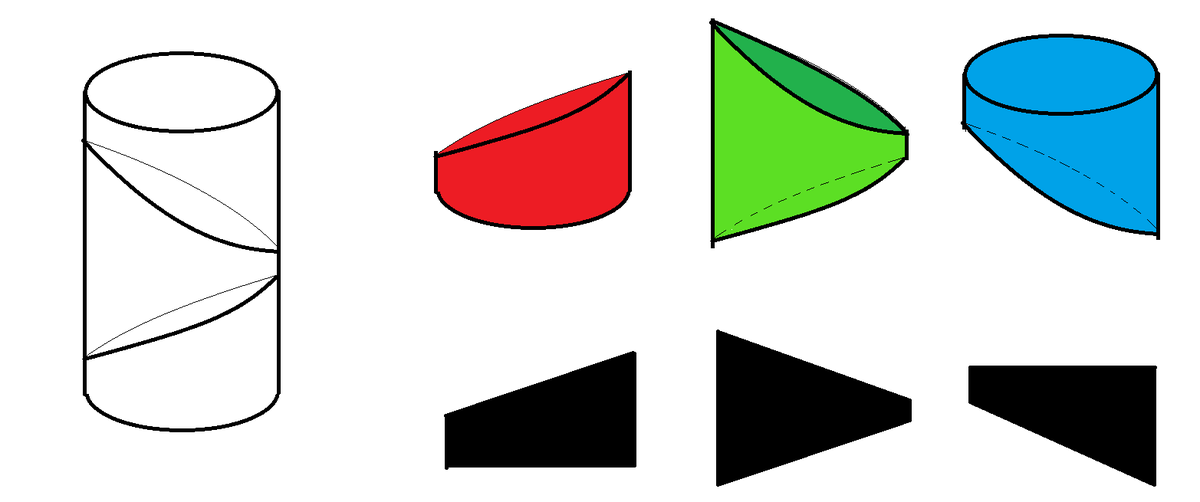
A cylinder is cut obliquely completely from left to right, resulting in 3 pieces.
By shining the light directly upon the lateral aspects of these figures, the 2D cross-section shadows can be obtained, as shown in black above.
If all the shadows have the same area, will the 3 figures have the same volume as well?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Perhaps an easier argument is to state that if the shadow is in the form of a trapezoid with base length a and b , then the length of points that are distance t from one of the base is equal to a + b . As such, regardless of which trapezoid area we're looking at, we can rearrange it to a cylinder of height 2 a + b .
My solution is a lot shorter tbh, so I'm not entirely sure it's correct. Anyway, there you go: So the volume of a cylinder is calculated, by taking the fundamental form and multiplying it by the height. So if all the shadows have the same area, if reshaped into a rectangle (with the broad of the circumference of the cylinder of course), they also have the same height. I hope you get what I mean.
The same then works for the parts of the cylinder of course, so they all have the same volume.
All trapezoids have the same height: the distance of two opposite, parallel line segments on the surface of the cylinder (2r). The areas of the three trapezoids are equal. The area of a trapezoid is the midsegment multiplied by its height, so the midsegments of the three trapezoids must be equal.
The volume of a cylindrical segment (when the cut planes don't cut the bases as defined above) is 2 h 1 + h 2 r 2 π , where h1 and h2 is the minimum and maximum heights of the cylindrical segment. Note that the midsegment of a shadow trapezoid is 2 h 1 + h 2 . So the volume of one cylindrical section is m r 2 π , which is the same for all bodies as their m and r values are equal.
Assuming the two cuts are made so that their normals are on the same plane. (That is, both cuts are "left-to-right", instead of one "left-to-right" and one "front-to-back".)
Without loss of generality, suppose the cylinder is x 2 + y 2 ≤ 1 , 0 ≤ z ≤ 3 , and the cuts have normal on the x z -plane. The shadows are the cross sections of each piece with the x z -plane. Each shadow is in the form of a trapezoid whose bases are on the line x = − 1 , y = 0 and on the line x = 1 , y = 0 . The height of the trapezoid is constant, 2 (because it's the distance between the two lines). Since the shadows have equal areas, this means the sum of the bases are constant. The sum of the bases over all shadows is 6 (each line contributes 3 units length, 0 ≤ z ≤ 3 ), so each shadow's sum of bases is 2. This means, the intersection of each shadow with the center x = 0 , y = 0 has length 1. Mark the points ( 0 , 0 , 1 ) , ( 0 , 0 , 2 ) ; each cut goes through one of these points (the lower cut passing through ( 0 , 0 , 1 ) and the upper cut passing through ( 0 , 0 , 2 ) ).
Now, take the plane z = 1 . The lower piece has some portion above this plane; rotate it 180 degrees around the axis y = 1 , z = 1 . It can be easily shown that this makes a perfect cylinder of height 1, so the volume of the piece is simply the volume of this cylinder, π . Similar with the upper piece, cutting the plane z = 2 and rotating through the axis y = 1 , z = 2 . The middle piece has the remaining volume, π , so all three pieces have the same volume.