Shadow doesn't always follow you!
 A small block can move in a straight horizontal line
A
B
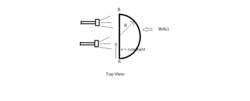
.Flash lights from one side projects its shadow on a curved vertical wall which has a horizontal cross section as a circle.
If tangential and normal acceleration of shadow of the block on the wall as a function of time can be represented as:
A small block can move in a straight horizontal line
A
B
.Flash lights from one side projects its shadow on a curved vertical wall which has a horizontal cross section as a circle.
If tangential and normal acceleration of shadow of the block on the wall as a function of time can be represented as:
a N = ( 2 R t − v t 2 ) c v R , a T = ( 2 R t − v t 2 ) g f R ( v t − R ) v e d .
Find ∣ c ∣ + ∣ d ∣ + ∣ e ∣ + ∣ f ∣ + ∣ g ∣
Details and Assumptions
-
As shown in figure v is the constant along A B .
-
Given Figure is top view of the setup.
-
c , d , e , f , g are natural numbers and e d , g f are in simplest forms.
-
a N , a T represent normal and tangential accelerations respectively.
-
you can neglect minus sign in accelerations due to directions.
The answer is 9.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
It is just not a level 5 problem, it must be level 4.
Easy but good problem.
I did in this way:

sin θ = R 2 v r t − v 2 t 2 . . . . . ( 1 ) cos θ = R R − v t . . . . . . . ( 2 )
differentiating equation 2nd w.r.t time (using chain rule)
− sin θ d t d θ = − R v ω = R v csc θ . . . . . . ( 3 ) a N = R ω 2 a T = R α ≡ R ω d θ d ω
Log in to reply
Yeah same I thought of this way just after posting the solution.It makes it much easier to solve but the concept is same.
I found the constants d,e,f,g by dimensional analysis, and c was guess, I know its not a proper method!! But I also tried to find it from conventional method
Did above solution helped u?If yes upvote it so others also see it and reshare the problem too.
Equation of curve ⇒ x 2 + y 2 = R 2
After time t
Co-ordinates of shadow ( 2 v t R − v 2 t 2 , v t − R )
Hence v x = d t d x = 2 v t R − v 2 t 2 v R − v 2 t and v y = v
Now a x = d t d v x = 2 v t R − v 2 t 2 2 3 − v 2 R 2 and a y = 0
Now we see that a x c o s ( z ) = a N and a x s i n ( z ) = a T
c o s ( z ) = R 2 v t R − v 2 t 2
s i n ( z ) = R v t − R .
Substituting values we get
a N = ( 2 R t − v t 2 ) v R , a T = ( 2 R t − v t 2 ) 2 3 R ( v t − R ) v 2 1 .
So c = 1 , d = 1 , e = 2 , f = 3 , g = 2
Hence ∣ c ∣ + ∣ d ∣ + ∣ e ∣ + ∣ f ∣ + ∣ g ∣ =9