Shadow Inside a Cube
A lamp is situated at a corner and shines inside the cube with edge length 6. There is also a square inside the cube whose vertices are located at the center of the 4 vertical faces. What is the area of its shadow?
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
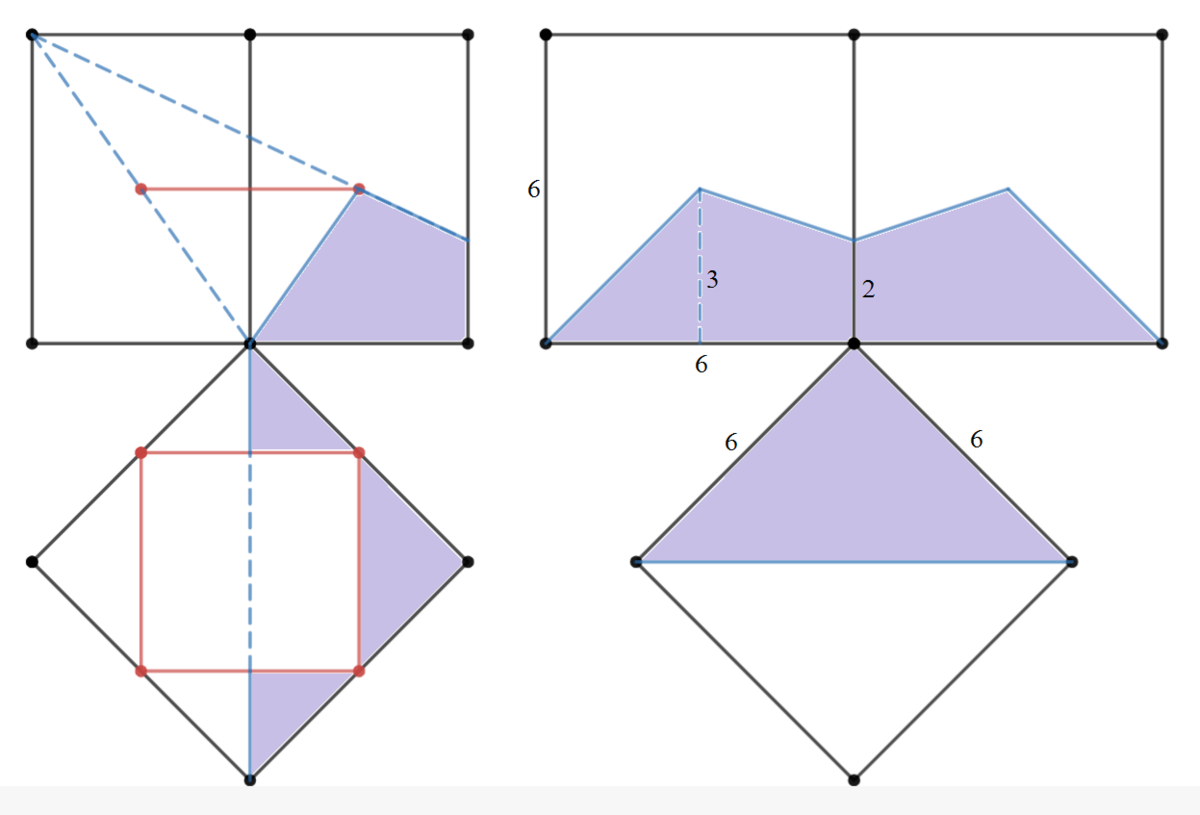
Don't have a 3-D graph app, I used the above 2-D drawing to solve the problem. The top-left plot is an elevation of the cube showing the point light source is at the top left corner the red line is the square in the cube. The bottom-left plot is a plan of the cube with the square in red. Grey indicates the shadow cast. The shadow on the two vertical square opposite the light source is each a truncated triangle. The show on the bottom square is an isosceles right triangle. The area of the shadow is:
A s h a d o w = 2 ( 2 3 × 3 + 2 3 + 2 × 3 ) + 2 6 × 6 = 4 2
Note that:
- the light or shadow will only be on 3 faces that do not have the lamp as a vertex (one bottom and 2 side faces).
- on each face, straight lines will project into straight lines.
- assuming the lamp is at a top, the nearest two vertices of the square are projected on opposite floor vertices,so the floor face of the cube is half lit.
- the midpoint of the far edge of the square is projected onto the far vertical edge of the cube, 3 1 from the bottom.
- drawing straight lines to the centre of a side face (adjacent to this vertical edge), we can see that each of these faces has 8 1 + 8 1 + 1 2 1 = 3 1 of its area shadowed.
In total we have ( 2 1 + 2 × 3 1 ) × 3 6 = 4 2 square units shadowed.
Following the labelling of figure 1, I L K L is the inscribed square, M and O are the midpoints of sides I L and J K respectively, P and Q are the midpoints of edges A E and C G respectively and N is the intersection point of A E with the extension of G M .
If the lamp is situated at G , then the shadow covers △ A B C on the bottom of the cube, plus the quadrilaterals A N L D and A N I B , the last two being congruent.
Now, the right triangles △ P M N and △ Q M G are similar, hence Q G P N = M Q P M ⇒ 3 P N = 3 1 ⇒ P N = 1 Thus, A N = A P − P N = 3 − 1 = 2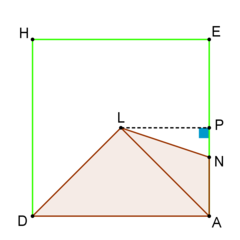 Figure 2
Figure 2
We divide the quadrilateral A N L D in two triangles: △ A L D and △ A N L (figure 2).
Evaluating areas we have [ A L D ] = 4 1 [ A E H D ] = 4 1 ⋅ 6 2 = 9 [ A N L ] = 2 1 A N ⋅ L P = 2 1 ⋅ 2 ⋅ 3 = 3 Moreover, [ A B D ] = 2 [ A B C D ] = 2 6 2 = 1 8 Summing up, the total area of the shadow is
[ A B D ] + 2 [ A N L D ] = [ A B D ] + 2 ( [ A L D ] + [ A N L ] ) = 1 8 + 2 ( 9 + 3 ) = 4 2