Shadow of a Circular Ring
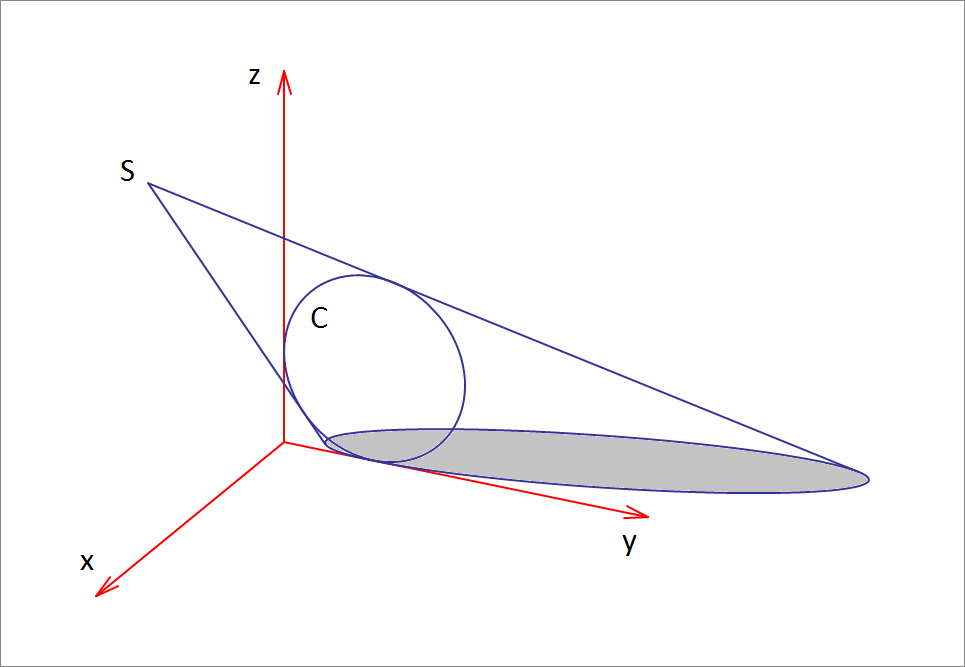
A point light source (like an LED) is located at S ( 5 , − 5 , 1 5 ) in a given coordinate frame. A circle C lies completely in the y z - plane, and has its center at ( 0 , 5 , 5 ) and a radius of 5 . The shadow of the circle onto the ground, which is the x y -plane is an ellipse . Find its area A , rounded to 3 decimal places.
The answer is 136.035.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The light rays between the point light source and points on the circle define an oblique cone, with its apex at the light source (point S ), and its base being the given circle C . The shadow is formed by the intersection of the x y -plane with this oblique cone of light rays.
This problem was addressed here .
The solution to that problem (with the necessary modifications) is repeated below for convenience.
Vectors connecting the apex S to points on the base are given by
v ( t ) = ( 0 , 5 cos t + 5 , 5 sin t + 5 ) − ( 5 , − 5 , 1 5 ) = ( − 5 , 1 0 + 5 cos t , − 1 0 + 5 sin t )
All the other points on the surface of the cone are scalar multiples of these vectors plus an offset of the apex coordinates.
We can think of this cone as a linear transformation of another arbitrary standard right circular cone.
Note first that v ( t ) can be written as
v ( t ) = cos t ( 0 , 5 , 0 ) + sin t ( 0 , 0 , 5 ) + ( − 5 , 1 0 , − 1 0 ) = v 1 cos t + v 2 sin t + v 0
An arbitrary standard right circular cone with apex at the origin, and a circular base centered at ( 0 , 0 , − h ) , and radius of base r has the following form of its lateral vectors
u ( t ) = cos t ( r , 0 , 0 ) + sin t ( 0 , r , 0 ) + ( 0 , 0 , − h ) = u 1 cos t + u 2 sin t + u 0
So we can write the vectors ( 0 , 5 , 0 ) , ( 0 , 0 , 5 ) , ( − 5 , 1 0 , − 1 0 ) (which are v 1 , v 2 , v 0 ) as a linear transformation (matrix multiplication) of the vectors ( r , 0 , 0 ) , ( 0 , r , 0 ) , and ( 0 , 0 , − h ) , ( which are u 1 , u 2 , u 0 ). In matrix form, this translates to,
V = A U
where V = [ v 1 v 2 v 0 ] and U = [ u 1 u 2 u 0 ]
The solution for the 3 × 3 matrix A is simply A = V U − 1
For computation, we can take h = 1 , r = 1 . It follows that points on our oblique cone are given by r = r 0 + A r ′ , where r 0 is the apex of the oblique cone, which is the point (5, -5, 15), and r ′ is the position vector of a point on the right circular cone.
Now, we know that the algebraic equation of points on the right circular cone are given by r ′ T Q ′ r ′ = 0 , where for the simple choice that we made of h = 1 , and r = 1 , we have,
Q ′ = ⎣ ⎡ 1 0 0 0 1 0 0 0 − 1 ⎦ ⎤
Substituting for r ′ , we obtain,
( A − 1 ( r − r 0 ) ) T Q ′ ( A − 1 ( r − r 0 ) ) = 0
which simplifies to,
( r − r 0 ) T Q ( r − r 0 ) = 0 where Q = A − T Q ′ A − 1
Now, we are ready to intersect this oblique cone with the cutting plane, which is the \( x y )- plane. The vector equation of any plane is
\( r = r_1 + W u \)
where r 1 is any arbitrary point on the plane, and W = [ w 1 , w 2 ] is a 3 × 2 matrix whose columns are arbitrary unit vectors that together with the normal to the plane form an orthonormal basis for R 3 .
In the case of the x y -plane, it is natural to choose r 1 = ( 0 , 0 , 0 ) , w 1 = ( 1 , 0 , 0 ) and w 2 = ( 0 , 1 , 0 ) .
Substituting this vector expression into the equation of the oblique cone, one obtains,
( r 1 − r 0 + W u ) T Q ( r 1 − r 0 + W u ) = 0
Expanding this quadratic form gives,
u T ( W T Q W ) u + 2 u T W T Q ( r 1 − r 0 ) + ( r 1 − r 0 ) T Q ( r 1 − r 0 ) = 0
Take u 0 = − ( W T Q W ) − 1 W T Q ( r 1 − r 0 ) , then the above equation becomes,
( u − u 0 ) T ( W T Q W ) ( u − u 0 ) = C
where the constant C is given by C = − ( r 1 − r 0 ) T Q ( r 1 − r 0 ) + u 0 T ( W T Q W ) u 0
Dividing by C , we obtain,
( u − u 0 ) T Q 1 ( u − u 0 ) = 1
where Q 1 = C 1 ( W T Q W ) .
The final step is to diagonalize Q 1 into Q 1 = R D R T . The diagonal elements of the diagonal matrix D are the eigenvalues of Q 1 which are the reciprocal of the square of the semi-major and semi-minorr axes lengths a and b of the resulting ellipse of intersection.
The area is given by π a b .
Let's now perform the above computations. We have
V = ⎣ ⎡ 0 5 0 0 0 5 − 5 1 0 − 1 0 ⎦ ⎤
U = ⎣ ⎡ 1 0 0 0 1 0 0 0 − 1 ⎦ ⎤
so that U − 1 = U = ⎣ ⎡ 1 0 0 0 1 0 0 0 − 1 ⎦ ⎤
Therefore,
A = V U − 1 = ⎣ ⎡ 0 5 0 0 0 5 − 5 1 0 − 1 0 ⎦ ⎤ ⎣ ⎡ 1 0 0 0 1 0 0 0 − 1 ⎦ ⎤ = ⎣ ⎡ 0 5 0 0 0 5 5 − 1 0 1 0 ⎦ ⎤
Its inverse is,
A − 1 = 5 1 ⎣ ⎡ 2 − 2 1 1 0 0 0 1 0 ⎦ ⎤
Now, let's compute matrix Q = A − T Q ′ A − 1 .
Q = 2 5 1 ⎣ ⎡ 2 1 0 − 2 0 1 1 0 0 ⎦ ⎤ ⎣ ⎡ 1 0 0 0 1 0 0 0 − 1 ⎦ ⎤ ⎣ ⎡ 2 − 2 1 1 0 0 0 1 0 ⎦ ⎤
Multiplying the last two matrices first, we obtain,
Q = 2 5 1 ⎣ ⎡ 2 1 0 − 2 0 1 1 0 0 ⎦ ⎤ ⎣ ⎡ 2 − 2 − 1 1 0 0 0 1 0 ⎦ ⎤
so that,
Q = 2 5 1 ⎣ ⎡ 7 2 − 2 2 1 0 − 2 0 1 ⎦ ⎤
Next, we compute the matrix W T Q W , this is given by:
W T Q W = 2 5 1 [ 1 0 0 1 0 0 ] ⎣ ⎡ 7 2 − 2 2 1 0 − 2 0 1 ⎦ ⎤ ⎣ ⎡ 1 0 0 0 1 0 ⎦ ⎤
Which is a straight forward computation. This comes to,
W T Q W = 2 5 1 [ 7 2 2 1 ]
Next, we compute the vector u 0 = − ( W T Q W ) − 1 W T Q ( r 1 − r 0 ) . Note that r 1 = ( 0 , 0 , 0 ) and r 0 = S = ( 5 , − 5 , 1 5 ) . Therefore,
u 0 = 3 1 [ 1 − 2 − 2 7 ] [ 7 2 2 1 − 2 0 ] ⎣ ⎡ 5 − 5 1 5 ⎦ ⎤
This comes to,
u 0 = [ − 5 1 5 ]
Now, we're ready to compute C = − ( r 1 − r 0 ) T Q ( r 1 − r 0 ) + u 0 T ( W T Q W ) u 0
This comes to,
C = − 2 5 1 ( 7 ( 2 5 ) + 1 ( 2 5 ) + 1 ( 2 2 5 ) + 4 ( − 2 5 ) − 4 ( 7 5 ) ) + 2 5 1 ( 7 ( 2 5 ) + 1 ( 2 2 5 ) + 4 ( − 7 5 ) )
Simplifying, we get,
C = − ( 7 + 1 + 9 − 4 − 1 2 ) + ( 7 + 9 − 1 2 ) = 3
Therefore, the matrix Q 1 = C 1 ( W T Q W ) is given by,
Q 1 = 7 5 1 [ 7 2 2 1 ]
The product of the eigenvalues of this matrix is equal to its determinant,
∣ Q 1 ∣ = a 2 b 2 1 = 7 5 2 3
Hence a b = 3 7 5 = 2 5 3 .
This means that the area is equal to π a b = 2 5 3 π = 1 3 6 . 0 3 5 when rounded to three decimal places.
The point ( 0 , 5 ( 1 + sin t ) , 5 ( 1 + cos t ) ) on C projects to the point ( x , y , 0 ) on the x y -plane, where x = 5 + 2 − sin t 3 ( − 5 ) = − 2 − sin t 5 ( 1 + sin t ) y = − 5 + 2 − sin t 3 5 ( 2 + cos t ) = 2 − sin t 5 ( 4 + sin t + 3 cos t ) and so x + 5 = 2 − sin t 5 ( 1 − 2 sin t ) y − 1 5 = 2 − sin t 5 ( − 2 + 4 sin t + 3 cos t ) and hence 7 ( x + 5 ) 2 + 4 ( x + 5 ) ( y − 1 5 ) + ( y − 1 5 ) 2 = 7 5 (The values of 5 and − 1 5 are found by averaging the minimum and maximum values of x and y respectively as t varies over [ 0 , 2 π ] , and the coefficients 7 , 4 , 1 are chosen to remove terms in cos t and sin t cos t in the numerator of the expansion 7 ( x + 5 ) 2 + 4 ( x + 5 ) ( y − 1 5 ) + ( y − 1 5 ) 2 ).
The eigenvalues of the matrix ( 7 2 2 1 ) are 4 ± 1 3 , and so we can find an X Y -axis system with origin at the point ( − 5 , 1 5 ) such that the equation of the shadow of C is ( 4 + 1 3 ) X 2 + ( 4 − 1 3 ) Y 2 = 7 5 which is the equation of an ellipse with semimajor and semiminor axes a , b , where a 2 = 4 − 1 3 7 5 b 2 = 4 + 1 3 7 5 and hence a b = 2 5 3 . The area of the ellipse is therefore π a b = 2 5 π 3 .