Shadow of an ellipsoid - modified version
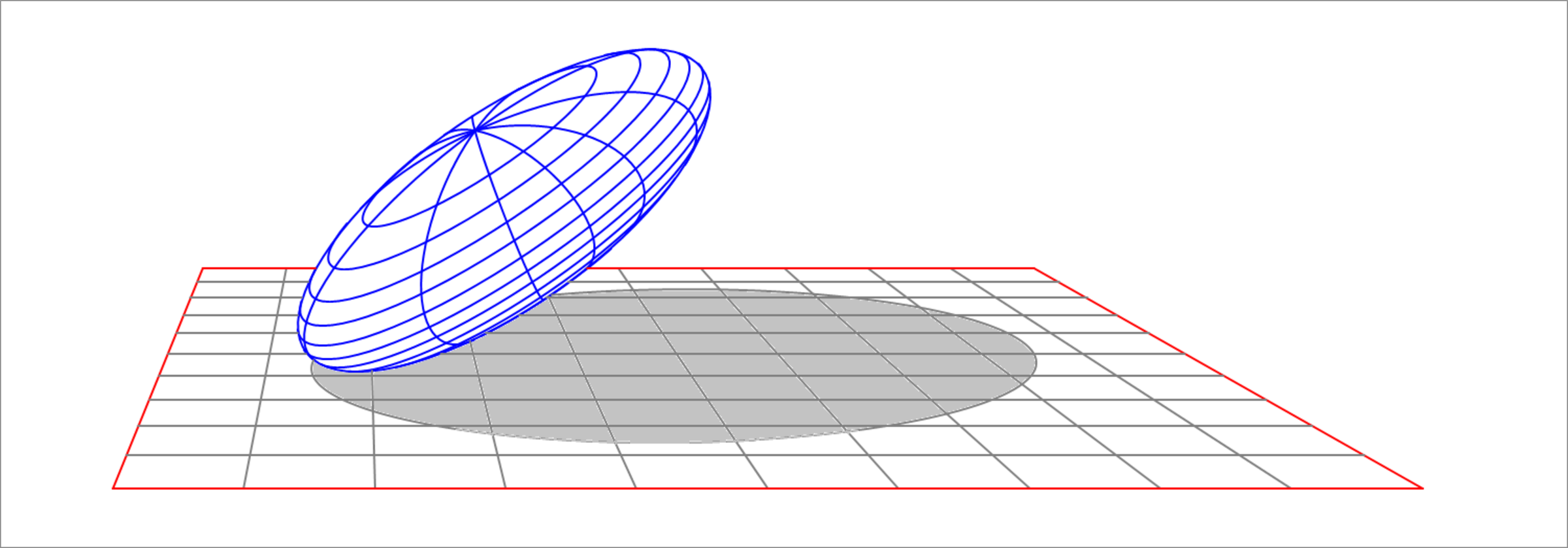
An ellipsoid centered at the origin has its first semi-axis of length 15 units along the unit vector , and its second semi-axis of length 30, along the unit vector , and its third semi-axis of length 10 along the unit vector . Now, with the orientation of the ellipsoid held fixed, translate the ellipsoid such that its lowest point (minimum z-coordinate) is placed at the origin of the Cartesian coordinate frame. Then, place a point light source at the point . The light source produces the shadow of the ellipsoid on the plane. Find the area of that shadow.
The answer is 2700.124.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If ( x ′ , y ′ , z ′ ) are the coordinates of a point, on the ellipsoid, with respect to u 1 , u 2 , u 3 , then we know that,
1 5 2 x ′ 2 + 3 0 2 y ′ 2 + 1 0 2 z ′ 2 = 1
Thus if we define r ′ = ( x ′ , y ′ , z ′ ) , and r = ( x , y , z ) ,then
r ′ T D e r ′ = 1 ,
where D e is a diagonal matrix whose diagonal entries are, in order, 1 5 2 1 , 3 0 2 1 and 1 0 2 1 . The relationship between r ′ and r is simply,
r = R e r ′ where R e = [ u 1 , u 2 , u 3 ]
The three columns of R e are orthonormal, hence R e − 1 = R e T , and thus, the equation of the ellipsoid is,
r T Q e r = 1 , where Q e = R e D e R e T
It is a simple matter to find the lowest point on the ellipsoid, because at that point the normal vector to the surface of the ellipsoid is pointing in the negative k direction, where k = ( 0 , 0 , 1 ) . Now, the normal vector is parallel to Q e r , hence, we have, Q e r = − α k for some positive constant α . Solving for r and plugging this into the ellipsoid equation, one finds that the lowest point r ∗ on the surface of the ellipsoid is given by
r ∗ = − k T Q e − 1 k 1 Q e − 1 k
Shifting the ellipsoid, such that the above found point becomes at the origin, one finds that the shift vector is r 0 = − r ∗ . The shifted image of a point r is the point r ′ = r + r 0 . Substituting for r into the ellispoid equation, we end up with,
( r ′ − r 0 ) T Q e ( r ′ − r 0 ) = 1
Dropping the primes off the primed variables, we end up with,
( r − r 0 ) T Q e ( r − r 0 ) = 1
And this is the final equation of ellipsoid that is now touching the x y plane at the origin.
The shadow of the ellipsoid on the x y plane is generated by the intersection of the x y plane and the non-uniformly scaled cone that is tangent to the ellipsoid, and which has its apex at the point ligth source p 0 . Tangency points on the ellipsoid are characterized by the vector equation,
( r − p 0 ) T Q e ( r − r 0 ) = 0
which can be manipulated as follows,
( r − r 0 + r 0 − p 0 ) T Q e ( r − r 0 ) = 0
And this simplifies to,
( r 0 − p 0 ) T Q e ( r − r 0 ) = − 1
This is an equation of a plane, thus all tangent points lie in a plane. Intersecting a plane with an ellipsoid was addressed here . The resulting ellipse of intersection defines the base of the general (non-uniformly scaled) cone, which has its apex at p 0 . The next and final task is to intersect this cone with x y plane, as was addressed in this problem . And this results in the shadow ellipse.
This is one way to proceed. The other way we can go is by transforming the ellipsoid into the unit sphere, then relating the original general cone to the regular cone resulting from the transformation. Recall that
( r − r 0 ) T Q e ( r − r 0 ) = 1
And that Q e = R e D e R e T = R e D e D e R e T
Thus, if define r ′ = D e R e T ( r − r 0 ) = A ( r − r 0 ) , then
r ′ T r ′ = 1 , i.e. r ′ is on the unit sphere centered at the origin. The corresponding
position of the point ligth source is p 0 ′ = A ( p 0 − r 0 ) . Our general cone is transformed
into a regular right circular cone, with apex p 0 ′ , and whose axis is along the vector p 0 ′ .
The semi-vertical angle of this right circular cone is simply θ c = sin − 1 ∣ p 0 ′ ∣ 1 . Therefore, the
equation of this cone is ( r ′ − p 0 ′ ) T R c D c R c T ( r ′ − p 0 ′ ) = 0
where D c is given by,
D c = ⎣ ⎡ cos 2 θ c 0 0 0 cos 2 θ c 0 0 0 − sin 2 θ c ⎦ ⎤
And the rotation matrix is of the form
R c = [ w 1 , w 2 , w 3 ]
such that w 3 is a unit vector in the direction of p 0 ′ (the axis of the right circular cone) and w 1 , w 2
are mutually orthogonal unit vectors that are also orthogonal to w 3 . Define Q c ′ = R c D c R c T ,
then we can, in a straightforward manner, find the corresponding matrix, in the original coordinates r
We start with,
( r ′ − p 0 ′ ) T Q c ′ ( r ′ − p 0 ′ ) = 0
And substitute
r ′ = A ( r − r 0 )
Hence, the equation of the original cone is (recall that p 0 ′ = A ( p 0 − r 0 ) ),
( r − p 0 ) T Q c ( r − p 0 ) = 0
where Q c = A T Q c ′ A . Now that we have the equation of the original (general, untransformed) cone, we intersect it with the x y plane, using the procedure outlined in the solution of this problem , and is repeated below for the reader's convenience.
The vector equation of any plane is
r = r 1 + W u
where r 1 is any arbitrary point on the plane, and W = [ w 1 , w 2 ] is a 3 × 2 matrix whose columns are arbitrary unit vectors that together with the normal to the plane form an orthonormal basis for R 3 .
In the case of the x y -plane, it is natural to choose r 1 = ( 0 , 0 , 0 ) , w 1 = ( 1 , 0 , 0 ) and w 2 = ( 0 , 1 , 0 ) .
Substituting this vector expression into the equation of the oblique cone, one obtains,
( r 1 − p 0 + W u ) T Q c ( r 1 − p 0 + W u ) = 0
Expanding this quadratic form gives,
u T ( W T Q c W ) u + 2 u T W T Q c ( r 1 − p 0 ) + ( r 1 − p 0 ) T Q c ( r 1 − p 0 ) = 0
Take u 0 = − ( W T Q c W ) − 1 W T Q c ( r 1 − p 0 ) , then the above equation becomes,
( u − u 0 ) T ( W T Q c W ) ( u − u 0 ) = C
where the constant C is given by C = − ( r 1 − p 0 ) T Q c ( r 1 − p 0 ) + u 0 T ( W T Q c W ) u 0
Dividing by C , we obtain,
( u − u 0 ) T Q 1 ( u − u 0 ) = 1
where Q 1 = C 1 ( W T Q c W ) .
The final step is to diagonalize Q 1 into Q 1 = R D R T . The diagonal elements of the diagonal matrix D are the eigenvalues of Q 1 which are the reciprocal of the square of the semi-major and semi-minorr axes lengths a and b of the resulting ellipse of intersection.
The area is given by π a b .