Shadows

Illustrate the problem.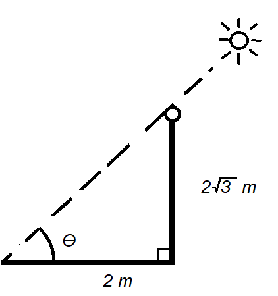

The opposite of angle $\theta$ is $2 \sqrt{3} m$ . The adjacent of angle $\theta$ is $2 m$ .

Reviewing trigonometric functions, $\tan \theta = \frac{opposite}{adjacent}$ is one of the trigonometric functions which needs opposite and adjacent. We can use $\tan \theta$ because we have the opposite of the angle $\theta$ , $2 \sqrt{3} m$ , and the adjacent of angle $\theta$ , $2 m$ .

$\tan \theta = \frac{opposite}{adjacent}$

Then, substitute $opposite$ in the $\tan \theta = \frac{opposite}{adjacent}$ with $2 \sqrt{3} m$ , and substitute $adjacent$ in the $\tan \theta = \frac{opposite}{adjacent}$ with $2 m$

$\tan \theta = \frac{2 \sqrt{3} m}{2 m}$

Cancel the $2$ s in the $\tan \theta = \frac{2 \sqrt{3} m}{2 m}$ because the fraction $\frac{2 \sqrt{3}}{2}$ has two 2s at the both numerator and denominator,

$\tan \theta = \sqrt{3} m$

Divide $\tan$ in the both sides of the equation, having the $\tan ^{-1}$

$\theta = \tan ^{-1} (\sqrt{3})$

Now we can use the calculator to input the above equation. The answer would be

$\theta = 60^\circ$

as shown in the figure ab =2 $\sqrt{3}$ and bc = 2 . tan d = $\frac{opp}{adj}$ = $\frac{2\sqrt{3}}{2}$ = $\sqrt{3} => d = 60^{0}$

Draw an triangle, write 2 squareroot 3 as opposite and 2m as adjacent, substitue the values and calculate using inverse tan-1(ans

x=tan-1(\frac{2/3}{2})

tan A (2(3)/2

angle of elevation = tan inverse into $\frac{2 square root 3}{2}$