Not Newton's Sum
Consider the cubic equation 2 4 5 x 3 − 2 8 7 x 2 + 9 9 x − 9 = 0 with roots α , β , γ . If
r = 0 ∑ ∞ ( α r + β r + γ r )
is of the form n m , where m and n are coprime positive integers, what is value of n + 1 m ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
With respect,could you explain that how to get the equation on the equation (1)?Why the numerator of the fraction is A0? Thank you!
Could you explain how you come to conclusion that roots are between -1 to 1. Because without that we can’t use infinite GP formula.
First simplify the infinite summation to 1 − α 1 + 1 − β 1 + 1 − γ 1 . The cubic equation can also be written as 2 4 5 x 3 − 2 8 7 x 2 + 9 9 x − 9 = 2 4 5 ( x − α ) ( x − β ) ( x − γ ) .
Simplify 1 − α 1 + 1 − β 1 + 1 − γ 1 to ( 1 − α ) ( 1 − β ) ( 1 − γ ) α γ + β γ + α β − 2 ( α + β + γ ) + 3 .
For the denominator plug in x = 1 . So ( 1 − α ) ( 1 − β ) ( 1 − γ ) = 2 4 5 4 8 .
Use vieta's formula to find out that β γ + α γ + α β = 2 4 5 9 9 , and that α + β + γ = 2 4 5 2 8 7 .
Then plug in those values for the numerator 2 4 5 9 9 − 2 ( 2 4 5 2 8 7 ) + 3 = 4 9 5 2 .
Then simplify 2 4 5 4 8 4 9 5 2 = 1 2 6 5 . So m = 6 5 and n = 1 2 . so n + 1 m = 1 3 6 5 = 5 .
This is not a genuine cubic equation.
alpha = 1/ 7
beta = 3/ 5
gamma = 3/ 7
1/ (1 - 1/ 7) + 1/ (1 - 3/ 5) + 1/ (1 - 3/ 7) = 7/ 6+ 5/ 2 +7/ 4 = 65/ 12
65/ (12 + 1) = 5
This is genuine cubic equation with three real roots: r = 0.6, 0.4286, 0.1429
Please explain p -1
I did it with Newton Sum method and cheated with a spreadsheet:
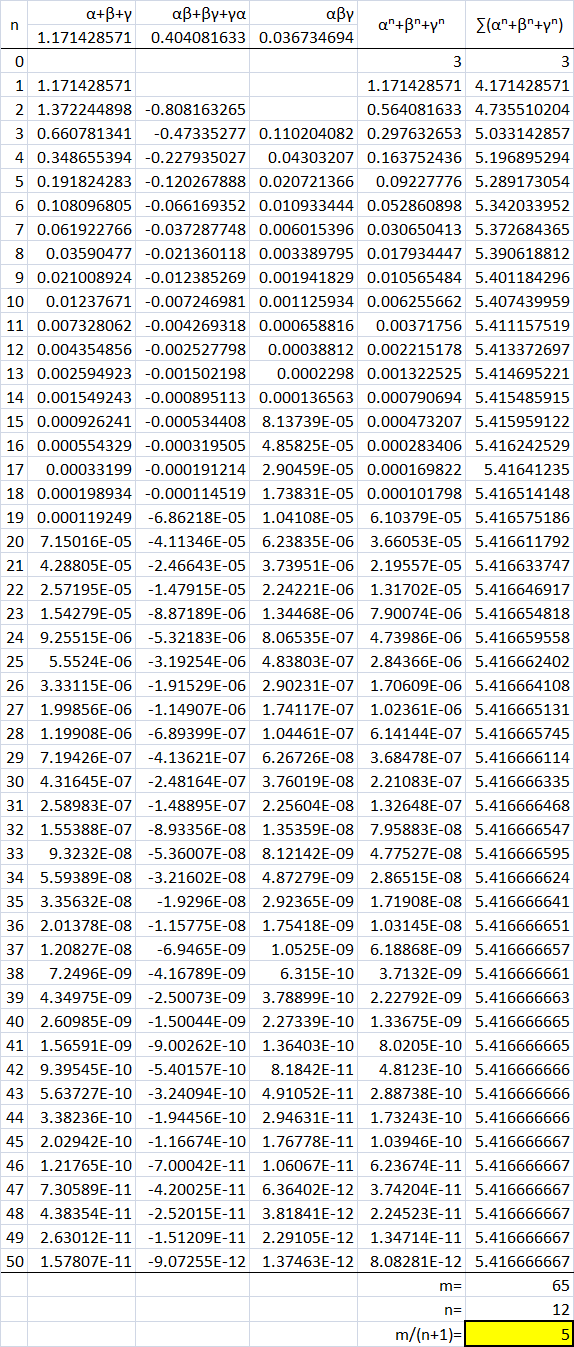
You Have Huge Patience :)
Log in to reply
Not really. Doing it in a spreadsheet is fast. You just formulate one row and just pull down to copy to the rest.
Well, I thought [ . . . ] is greatest integer function, so I got n m = 4 , m = 4 , n = 1 , n + 1 m = 2 which was unfortunately there in options! 😢
this sheet BLOWS my MIND....!!! :P
f(x)=(x-a)(x-b)(x-c) Take log and differentiate f'(x)/f(x) =(x-a)^-1+(x-b)^-1+(x-c)^-1 =1/x(1+a/x+a^2/x^2 ...)+1/x(1+b/x+b^2/x^2 ...)+1/x(1+c/x+c^2/x^2 ..) Now just put x=1 so m/n = f'(1)/f(1).=65/12 and m/n+1 =5 This solution has a advantage as if roots are more than 3 say n then also ans. will be f'(1)/f(1) you don't need deal with them individually making equations and solving them . This give solution to whole class of such problems.
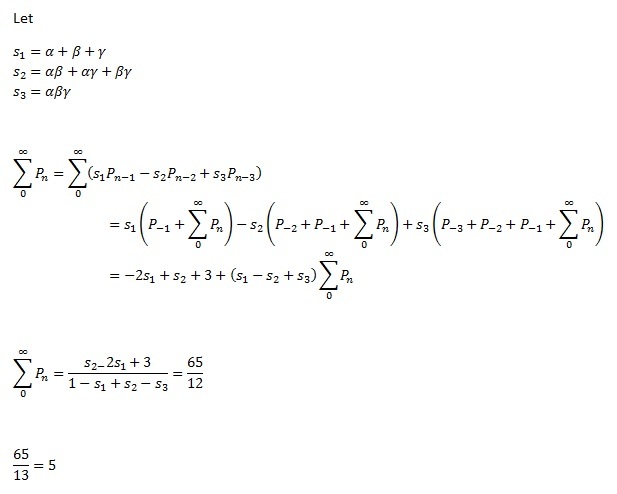

Please upvote if you like it
Let α = a , β = b , γ = c
Now as we know that the individual roots a , b , c are making a geometric progression i.e we have to find
a 0 + a 1 + a 2 . . . . a n + b 0 + b 1 + b 2 . . . . b n + c 0 + c 1 + c 2 . . . . c n
which will give us
1 − a a 0 + 1 − b b 0 + 1 − a c 0
1 − a 1 + 1 − b 1 + 1 − c 1 . . . . . . . . . . . . ( 1 )
By vieta we have
a + b + c = 2 4 5 2 8 7 , a b + b c + c a = 2 4 5 9 9 , a b c = 2 4 5 9
on simplifying . . . . . . . . . . ( 1 ) we get
1 − ( a + b + c ) + a b + b c + c a − a b c 3 − 2 ( a + b + c ) + a b + b c + c a
Now plugging
1 − ( 2 4 5 2 8 7 ) + 2 4 5 9 9 − 2 4 5 9 3 − 2 ( 2 4 5 2 8 7 ) + 2 4 5 9 9
which gives us 1 2 6 5
here m = 6 5 , n = 1 2
∴ n + 1 = 1 3
∴ n + 1 m = 1 3 6 5 = 5