Shapes Of Constant Width

In order to touch the opposite side, each arc is 60 degrees with a radius that is equal to the side length of the square.

Therefore the perimeter $= 3 \times (2 \times \pi \times 4) \times \frac{ 60 ^ \circ } { 360^ \circ } = 4 \pi.$

every arc of this reuleaux triangle is a segment of a circle of radius 4...(i figured it out since it is this triangle is of continuous width..now to find the perimeter of a single arc we can apply the formula (radius x radians subtended at the centre of the circle) which means $4 \times \pi / 3$ . Since there are 3 arcs, multiply this by 3 to obtain a perimeter of $4 \pi$ .

A reuleaux triangle is created by starting from an equilateral triangle and creating an arc from each corner between the two opposite corners. This means you are simply creating 3 arcs. The area for an any arc is $\frac{\theta} {360} \times 2 \times pi \times r$ (in degrees). As it is an equilateral triangle the angle is then 60. As the square has a perimeter of 16, each side must be 4cm so the height of the curve or the radius is 4. As we need 3 equal curves the equation we now get is $\frac{60}{360} \times 2 \times 4 \times 3 \times pi$ or just $pi \times 4$ . So the answer is 12.6 .

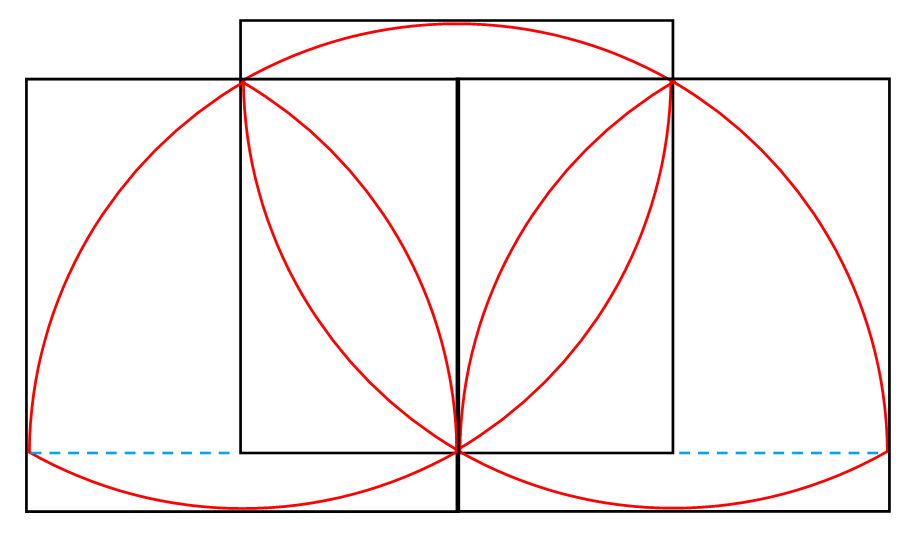The perimeter of the Reuleaux Triangle is equal to the arc length of a semicircle with radius 4. i.e. 4π。

This directly follows from Barbier's Theorem ................!!!

$Perimeter\quad of\quad Reuleaux\quad triangle\quad =\quad \pi w,\ where\quad w\quad is\quad the\quad constant\quad width.$ Here, the constant width of the Reuleaux triangle = side of square $Side\quad of\quad square\quad =\quad \frac { Perimeter }{ 4 } \quad =\quad 4cm$

So, the perimeter $=\frac { 22 }{ 7 } \times \quad 4\\ =\frac { 88 }{ 7 } \\ =12.5714286$

By Barbier's Theorem, the perimeter is just $\pi \times{r}$ where $r$ is the radius of the series of arcs that make up the Reuleaux triangle. Thus, the answer is approximately $\boxed{12.56}$ .

I just imagined that the perimeter of the triangle is the same as the perimeter of circle with the same width.

so r=2, p= 2pi*r

s = 16/4 = 4

the perimeter is :

p = πs = 12.566

The Reuleaux triangle's perimeter is actually three parts of a circle. Since the perimeter of the square is 16, its side is equal to 4 units. In the first picture the, Reuleaux triangle is placed such that the radius of the circular arc touching the bottom side is equal to the length of the side, as one corner touches the opposite side. Therefore we know that the radius of the three arcs (by drawing similar conclusion for the other two) is 4 units. Now, the given triangle is equilateral as all three arcs are of equal lengths. Hence the angle made by the arc at the opposite vertex is 60 degrees or π/3. Hence the perimeter of one arc by using, l=Rxθ, we have, l=4xπ/3 But there are three arcs, therefore, total perimeter is given by 3x4xπ/3 =4xπ =12.56 approximately.

Area of a reuleaux triangle is $\frac{\pi s^2}{4}$

http://en.wikipedia.org/wiki/Reuleaux_triangle