You Need To Look Everywhere
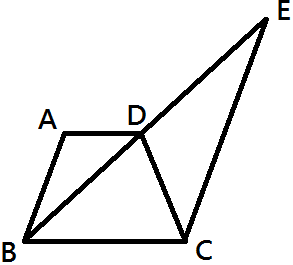
In the above figure, A B C D is a trapezium, B D E is a straight line and A B ∣ ∣ C E . If B D = 8 and D E = 7 , find the ratio of the area of Δ A D B to the area of Δ C D E .
Note : The figure is not drawn to scale.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
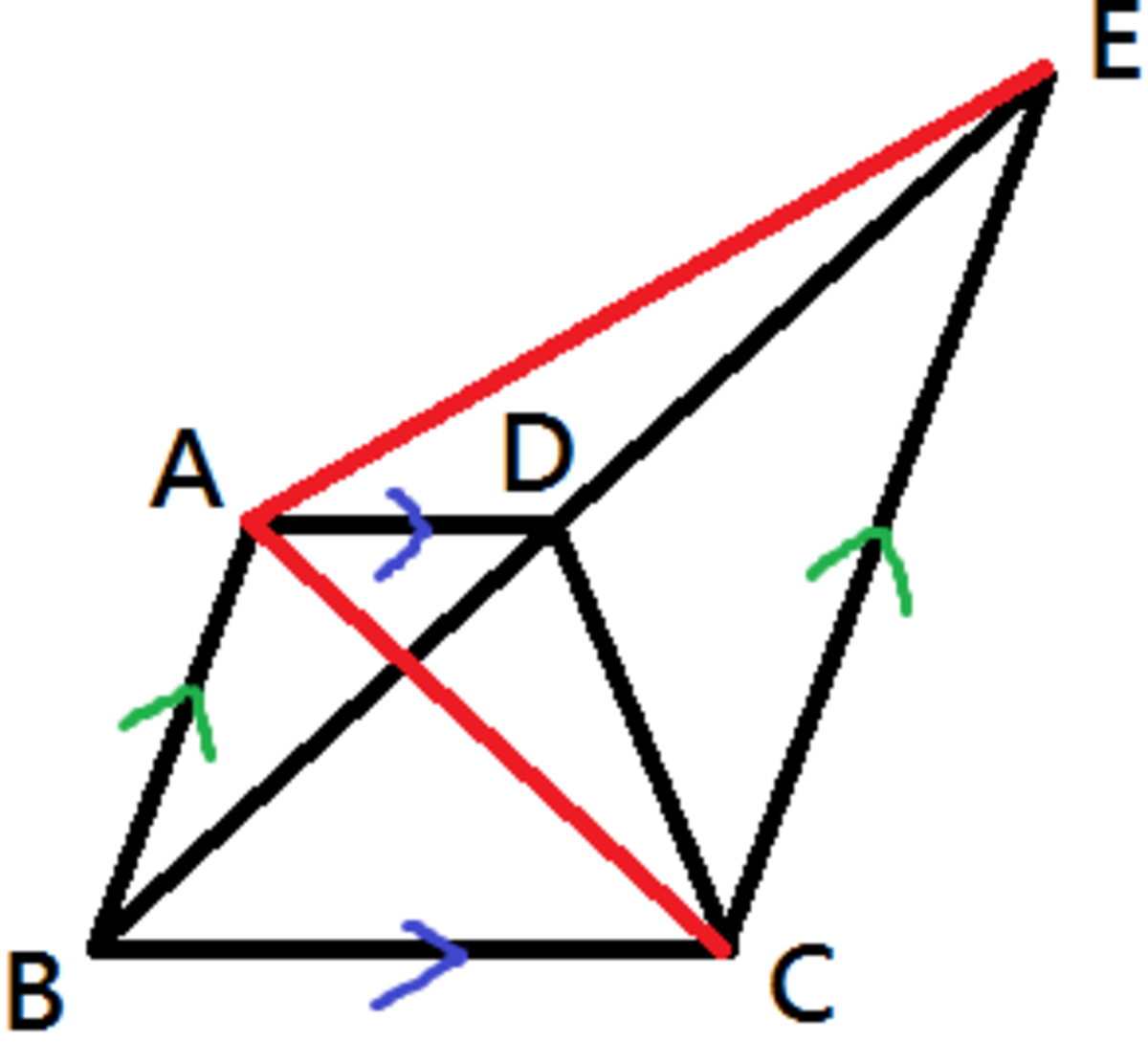
Let [ A B D ] = x , [ C D E ] = y so the problem asks us to find y x .
Since A D ∣ ∣ B C we have [ A B D ] = [ A D C ] = x as they have same base and same height.
Since D E B D = 7 8 we have two area relations:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ [ A D E ] [ A B D ] = 7 8 ⟹ [ A D E ] x = 7 8 ⟹ [ A D E ] = 8 7 x [ C D E ] [ B D C ] = 7 8 ⟹ y [ B D C ] = 7 8 ⟹ [ B D C ] = 7 8 y
Now since A B ∣ ∣ C E we have:
[ B C E ] = [ A C E ]
⟹ [ B D C ] + [ C D E ] = [ A D C ] + [ A D E ] + [ C D E ]
⟹ [ B D C ] = [ A D C ] + [ A D E ] Substituting the above computed areas in terms of x , y :
⟹ 7 8 y = x + 8 7 x ⟹ 7 8 y = 8 1 5 x
⟹ y x = 1 5 × 7 8 × 8 = 1 0 5 6 4 which was what we had to find. Cheers!
Notation: Denote [ A B C ] as the area of Δ A B C .
Moderator note:
Good approach. This solution could be simplified further by making better use of the observations with parallel lines / ratios that you already established. For example, consider the following product:
[ A B E ] [ A D B ] × [ A B C ] [ A B E ] × [ E B C ] [ A B C ] × [ E D C ] [ E B C ]
I Love this solution, thanks
Log in to reply
Glad to hear that. Please do upvote, it motivates me to post more :)
Can you please explain me how you get [ A D E ] [ A B D ] = [ C D E ] [ B D C ] = 7 8 ?
Log in to reply
Triangles sharing the same vertex and collinear bases have their areas in proportion of their bases since their height is the same! :rage:
Given two side-lengths
x
and
y
and the contained angle
θ
, the area of a triangle is
2
1
x
y
sin
(
θ
)
.
Since ∠ A B D = ∠ D E C and A B = 1 5 8 C E , the ratio of the areas is: 2 1 ⋅ 7 ⋅ C E ⋅ sin ( ∠ A B D ) 2 1 ⋅ 8 ⋅ 1 5 8 C E ⋅ sin ( ∠ A B D ) = 1 0 5 6 4
By the way, the term "trapezium" is defined differently in the U.S. and the U.K.

Draw a line DF, which parallels to AB and EC. Mark all the information provided, you will have a figure like the following: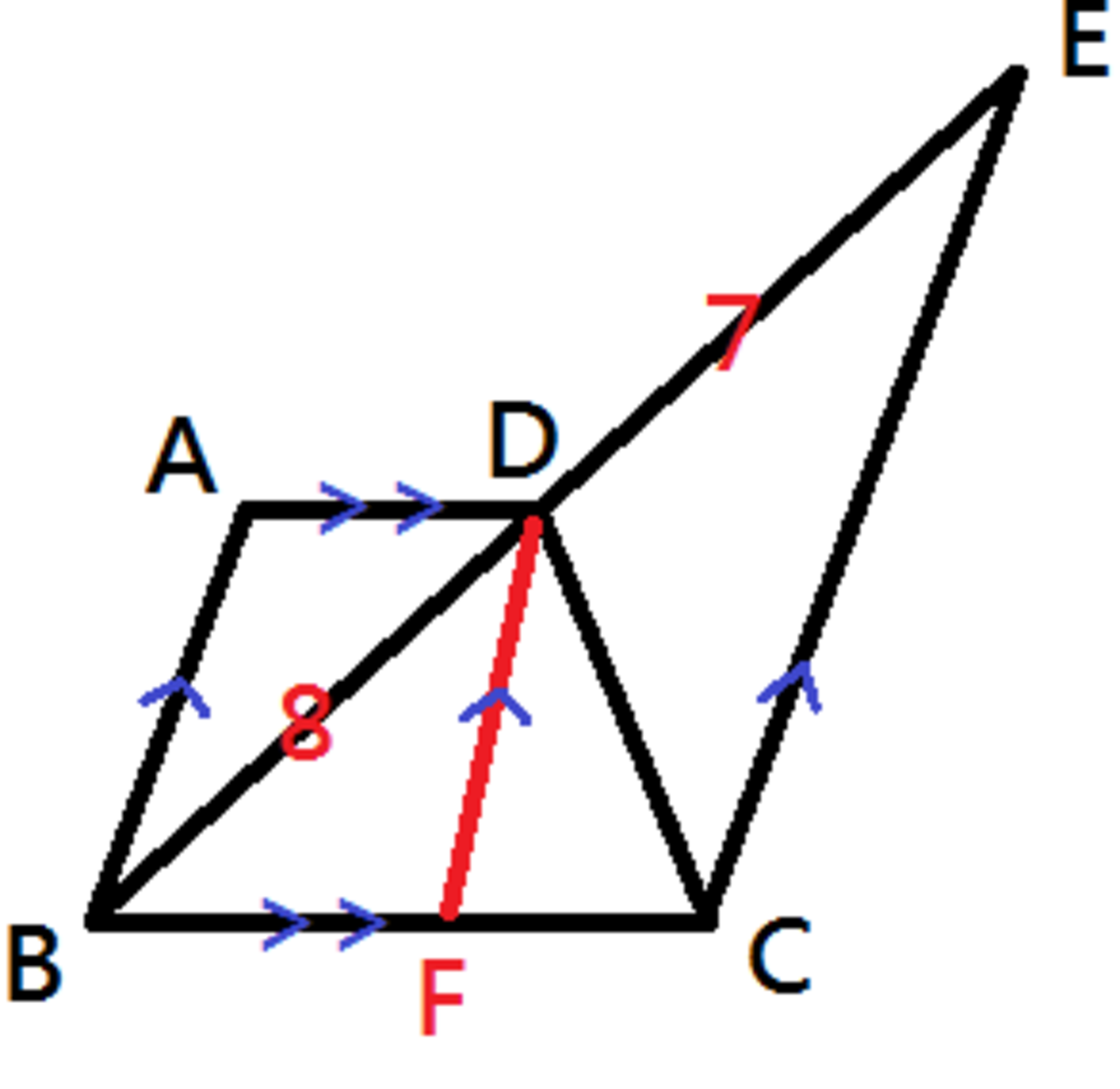
Note that the length of BF and FC are in ratio 8:7 (Intercept theorem, DF//EC). △BCD and △ECD share the same height DC, so that the ratio of the area of △BCD and the area of △ECD is also 8:7.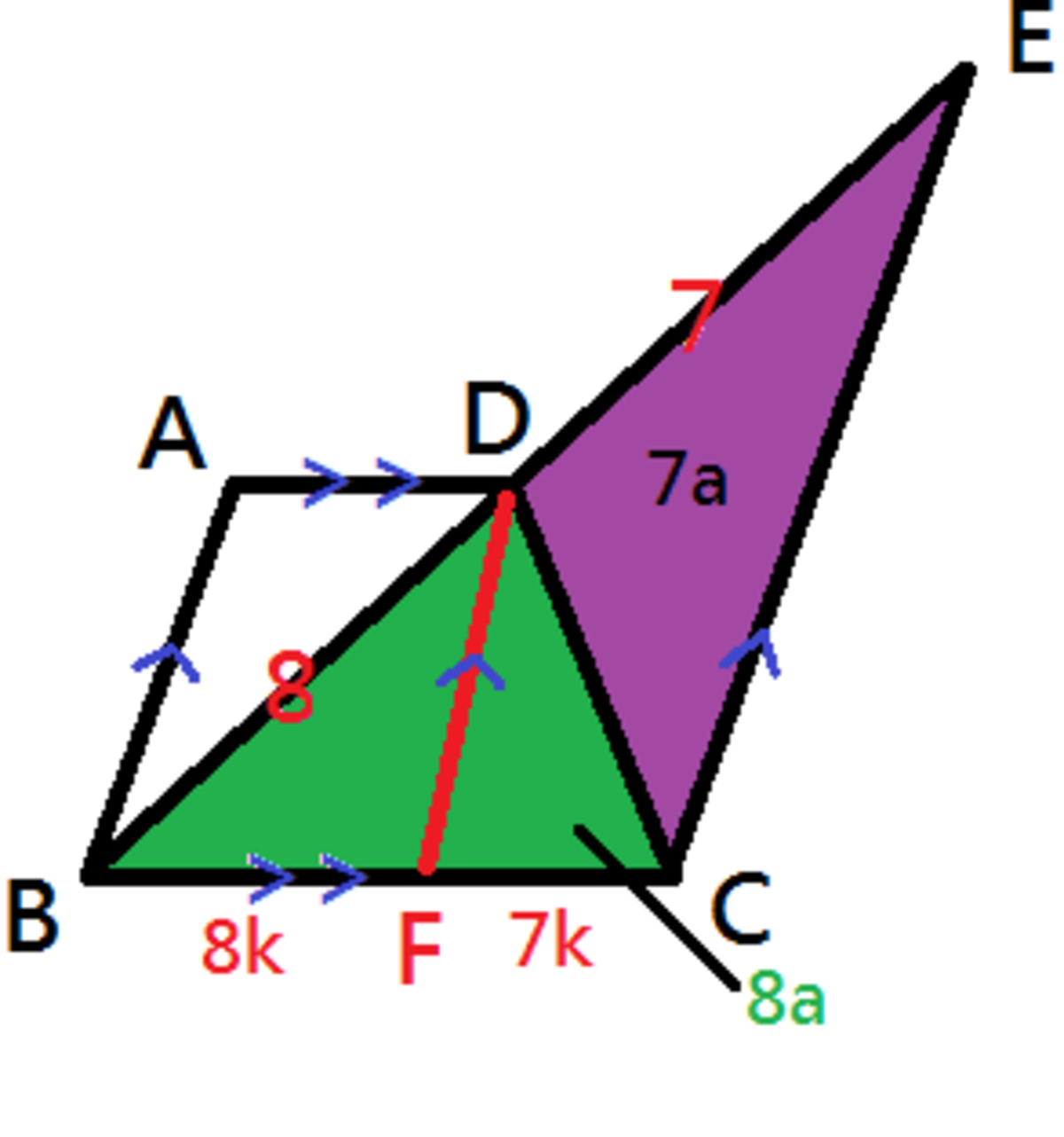
Note: The following areas are in ratios only.
△BCD is divided into two triangles by DF, △BDF and △FDC.
The area of △BDF = 8 + 7 8 ・ 8 = 1 5 6 4
The area of △FDC = 8 + 7 8 ・ 7 = 1 5 5 6
As ABFD is a parallelogram, area of △BDF = △BDA = 1 5 6 4 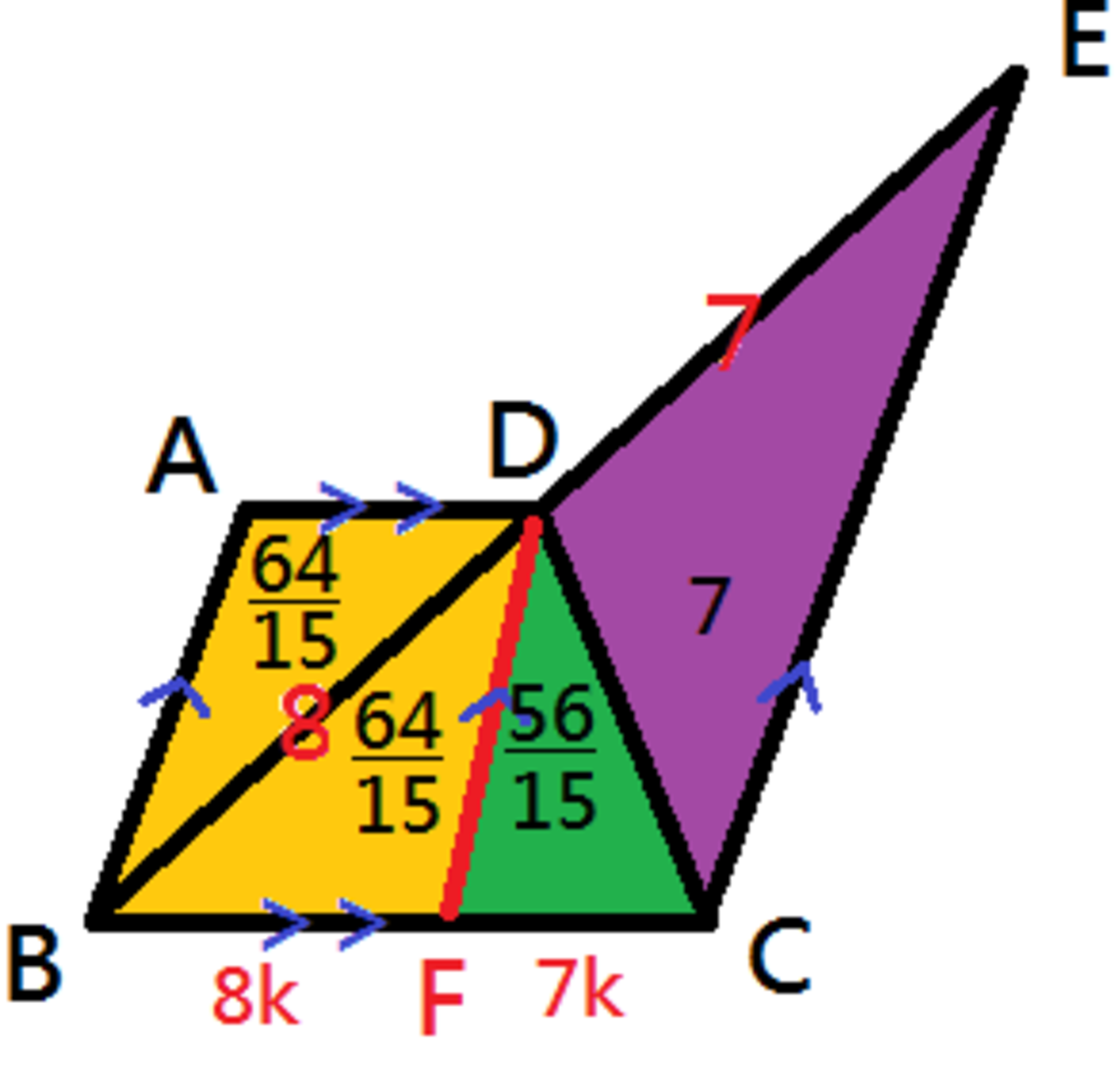
Area of △ABD : △CDE = 7 6 4 / 1 5 = 64 : 105