Let $f(n)$ be the fraction of the pie the $n^{\text{th}}$ person gets. Then $f(n) = \displaystyle \frac{n}{100} \prod_{i=0}^{n-1} \frac{100-i}{100}$

Consider $\frac{f(n+1)}{f(n)} = \frac{100-n}{100} \cdot \frac{n+1}{n}$ Then $\frac{f(n+1)}{f(n)} >1$ if and only if $\frac{100-n}{100} \cdot \frac{n+1}{n} > 1 \iff (100-n)(n+1) > 100 n \iff 100 - n -n^2 >0$ Now one root of the polynomial $100-n-n^2$ is negative while the other is $\approx 9.512$ . This means the ratio $\frac{f(n+1)}{f(n)} >1$ as long as $n \leq 9$ . So $f(n)$ is increasing until it reaches $n=10$ . After that it decreases.

Thus the $\boxed{10^{\text{th}}}$ person gets the largest part of the pie.

Let $f(n)$ be the fraction of the pie $n^{th}$ person gets. Let 1 denote the amount of pie in the starting.

So, $f(n) = \displaystyle\frac{n}{100}\Bigg(1 - \sum_{i=1}^{n-1}f(i)\Bigg)$ for $n \geq 2 \qquad\qquad\dots \text{Eq. 1}$

Also, $f(n) = \displaystyle\sum_{i=1}^{n}f(i) - \sum_{i=1}^{n-1}f(i)\qquad\qquad\dots\text{Eq. 2}$ .

Using Eq. 1 in Eq. 2 , we get

$f(n) = 100\Bigg( \frac{f(n)}{n} - \frac{f(n+1)}{n+1}\Bigg) \Rightarrow \frac{f(n+1)}{f(n)} = \frac{(100-n)(n+1)}{100n}$

Now we have to find maximum value of $n$ such that $f(n+1) \geq f(n)$ $i.e. \ \frac{f(n+1)}{f(n)} \geq 1$

$\Rightarrow \frac{(100-n)(n+1)}{100n} \geq 1$ $\Rightarrow (100-n)(n+1) \geq 100n \Rightarrow n^2 + n - 100 \leq 0$

The positive root of this equation $\approx 9.51$ . So maximum value of $n$ can be $9$ .

And so, $f(10) \geq f(9)$ . Hence $10^{\text{th}}$ person will get the largest piece of pie.

I got lazy at deriving formula, so I used excel. Column A as guest number, Column B (amount of pie) and C (pie remaining) with formulas as shown, and dragged the them down all the way to 100th guest, and plotted graph, to reach answer -->10

Bashed with a calculator. Trivial.

When it is the turn of number m, a certain part, 'r', of the pie is left.

Person number m gets 'r' multiplied by (m/ 100), i.e.

= r*(m/100)

which is the formula for m per cent of 'r', and the amount of pie left is

= r *(100-m)/100.

When it comes to the turn of the next person m + 1, he will get

= r* ((100-m)/100)* ((m+1)/ 100).

Therefore person m+1 gets more than person m, if

(100-m)/100)* ((m + 1)/100) > m/100.

This reduced to the inequality

100 - m- m^2 > 0 ,

is true for m = 1, 2...., up to 9.

In other words, the amount of pie taken by each person keeps on increasing until the 9th person , but from the 10th person and beyond the amount is smaller.

Therefore, we conclude , number 10 gets the largest amount.

This above solution is discussed for the same puzzle which appeared recently in Guardian paper.

Solution 1

Some Haskell code. (Type annotations omitted for space and not needed since Haskell has type inference).

1
2
3
4
5
6
7
8

import Data.List (maximumBy)
import Data.Ord (comparing)

main = print result
result = snd $ maximumBy (comparing fst) $ zip (map (f 100) [1..100]) ([1..100])
-- The fraction of the pie received when there are `n` people, the first
--  getting `1 / n` of the whole, and the `i`th getting `i / n` of what remains.
f n i = (i / n) * product [ 1 - (j / n) | j <- [1..(i-1)] ]

Output:

1

10

Solution 2

Let $f(j)$ be the fraction of the pie received by the $j$ th person. Then we have $f(j) = g(j) h(j)$ , where

$\begin{aligned} g(j) & = \prod^{j-1}_{i=1} \left( 1 - \frac{j}{100} \right) \\ h(j) & = \frac{j}{100} \end{aligned}$

Let $\Delta$ denote the finite difference operator. Then $\Delta f(j) = g(j) \Delta h(j) + \Delta g(j) h(j+1)$ . Since $\Delta h(j) = \frac{1}{100}$ and

$\begin{aligned} \Delta g(j) & = g(j+1) - g(j) \\ & = g(j) \left( 1 - \frac{j}{100} - 1 \right) \\ & = - \frac{j}{100} g(j), \\ \end{aligned}$

we have that $\begin{aligned} g(j) \Delta h(j) + \Delta g(j) h(j+1) & = \frac{1}{100} g(j) - \frac{j}{100} \frac{j+1}{100} g(j) \\ & = \left[\frac{1}{100} - \frac{j^2 +j}{10000} \right] g(j) \\ \end{aligned}$

Since $g(j)$ is positive, we have $\left[\frac{1}{100} - \frac{j^2 +j}{10000} \right] g(j) > 0$ when $\frac{1}{100} > \frac{j^2 +j}{10000}$ , or equivalently $1 > \frac{j^2 + j}{100}$ , or equivalently $100 > j^2 + j$ . When $j$ is restricted to be an integer, this happens precisely when $j < 10$ , so $j = 10$ is the first integer at which $\Delta f$ is decreasing. This tells us immediately that $n = 10$ , since all values of $f(j)$ with $j < 10$ are smaller since $f$ is increasing on them and all values of $f(j)$ with $j > 10$ are smaller since $f$ is decreasing on them.

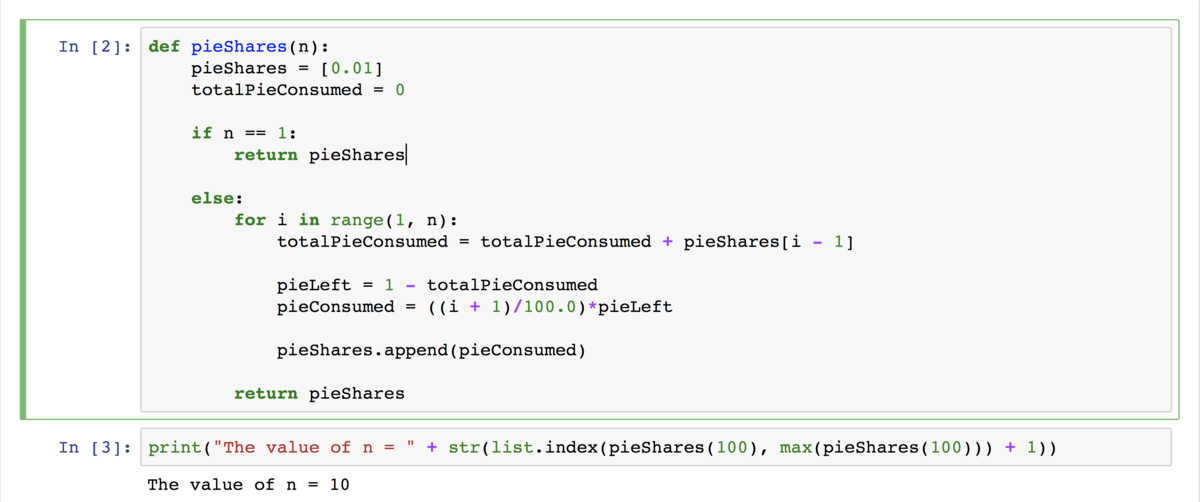
i uh... just wrote a matlab code... is that cheating?

pie(1)=100;

for i=1:100

cut(i)=i/100;

cutofpie(i)=pie(i)*cut(i);

pie(i+1)=pie(i)-cutofpie(i);

end

max(cutofpie) %now look in the variable cutofpie for the entry at which the max value is in.

If we simplify the problem and think about ten guest, who's proportions increase by 10% instead of 1% of what's left, calculate how much each of those gets and plot it, we get the brown function. Its maxima is at around 30% so the third guest gets the biggest part. 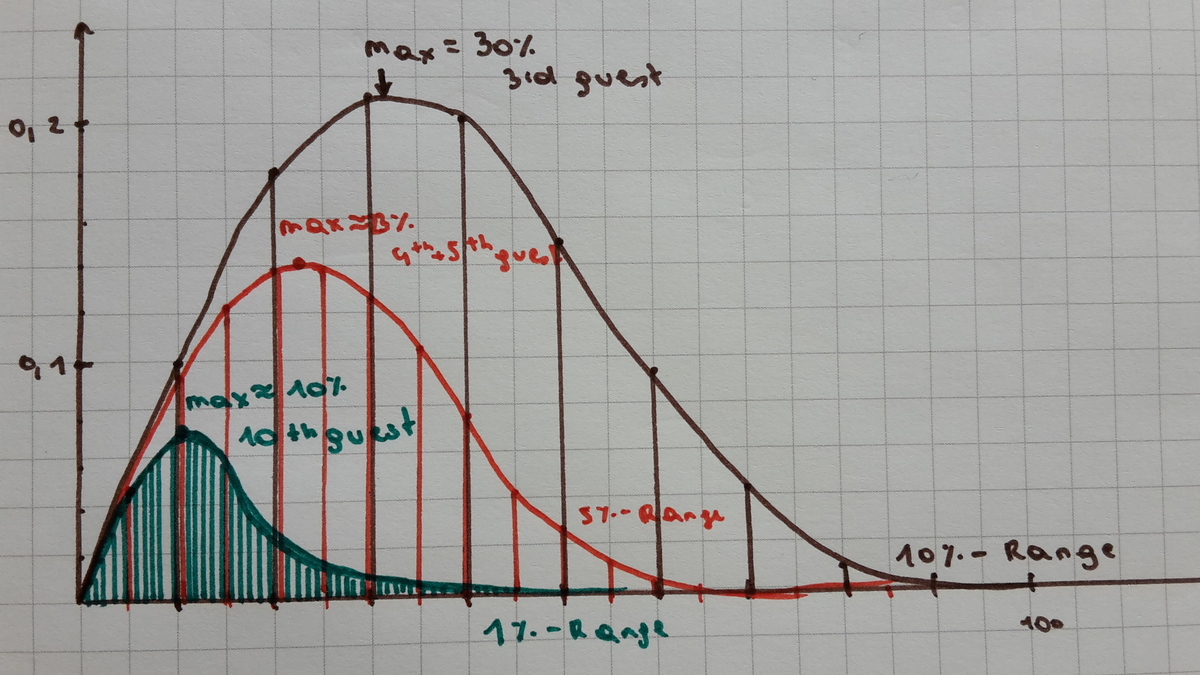When we decrease the percentage to 5% (red line) and in the end to 1%, we see that the maxima shifts, as more stuff is taken from the cake in the beginning and therefore sooner less is left. Therefore the maxima, where the percentage is big enough to get more than the person before, but the cake is still large enough to not outweigh the increase in percentage, is shifted to the left. To about 10%. That is why the tenth person gets the most cake with 0,628% of the total cake.

THIS "big" piece of cake would leave me still hungry ;)

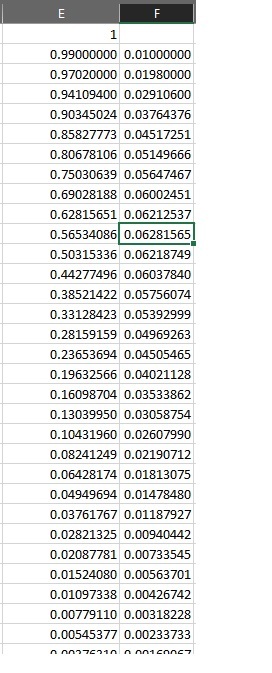
I used Excel, set up the following way: ||Guest #||Share||Pie Remaining|| ||1||=A2 A2/100||=1-B2|| ||2||=(C2 A3/100)||=C2-B3|| ... ||100||=(C100*A101/100)||=C100-B101|| |

Graphing can also be used to solve this problem.

Let $\displaystyle f(x)=\prod_{n=1}^{x}1-\frac{n}{100}$

A plot of this function: 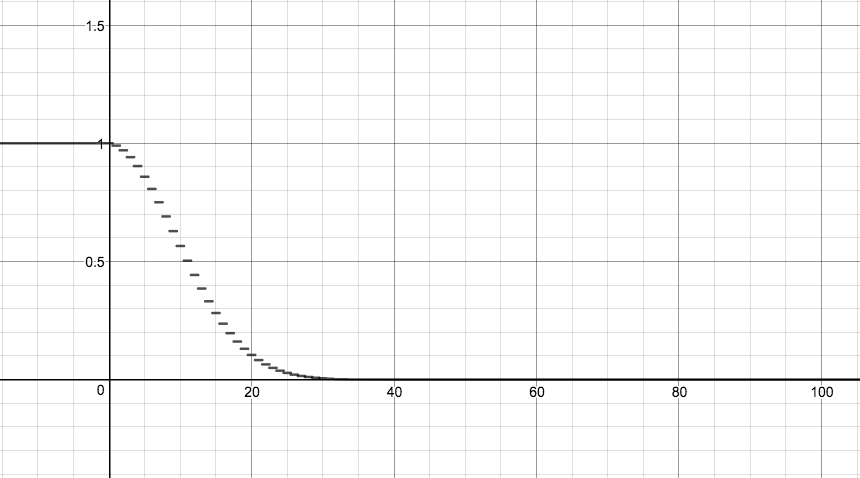Source: https://www.desmos.com/calculator/w8o7mdfuc2

Let $j(x) = f(x-1)-f(x)$

The function $j(x)$ shows the difference between two consecutive values. The peak of the graph of the function $j(x)$ shows the number of the guest that took the largest piece of the pie.

The plot of the function $j(x) = f(x-1)-f(x)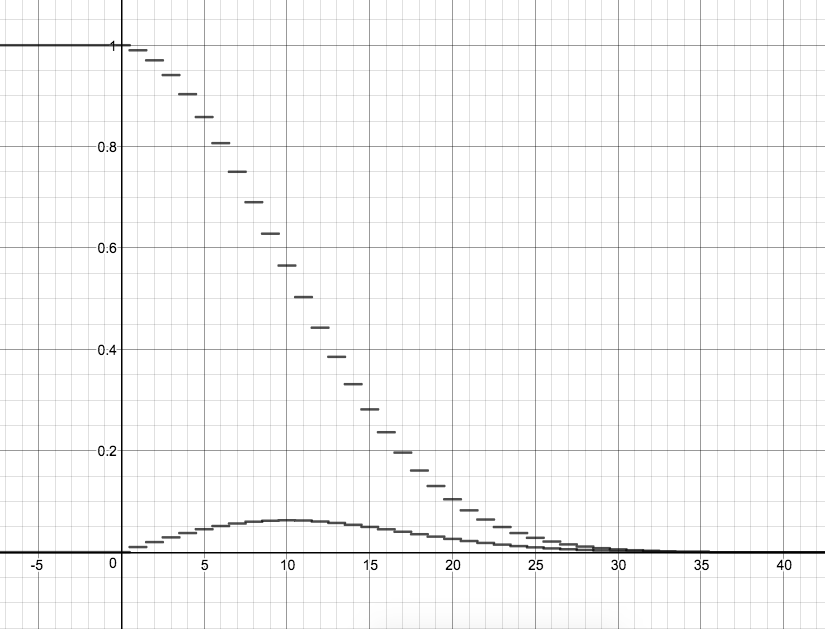$ : Source: https://www.desmos.com/calculator/w8o7mdfuc2

The peak of the graph is at $10$ and thus the $10$ th person is the one who took the largest piece of the pie. The answer is $\fbox{10}$ .

NOTE: Both function are not continuous and that is why they are "cut" between each whole number.

Here's a wicked and intuitive way to figure out this problem!

Consider the following as if it were a new problem:

1. For the first few $n$ , each slice of pie will be just slightly less than $n$ % of the pie in size.

2. The size of each slice of pie will only start to decrease when half the pie has been eaten.

Given this, how many slices do we eat before half the pie is gone?

For complicated reasons, the simplified logic of the new problem illustrated here holds when applied to the main problem. Good luck!

We can model the amount of pie left after x people take their share with a recursive function:

f(x) = f(x-1) - f(x-1)*(x/100), f(0) = 1.

This can be simplified to this:

f(x) = (f(x-1)(100-x))/100

If we extend this function out, evaluating it at f(1),f(2), etc., then you notice a pattern develops:

f(x) = (99!/(100-x)!)*(1/100^(x+1))

If you want to find out how much x person takes, simply multiply the amount of pie by the persons number over 100:

f(x) = 99!/((100-x)!*100^x)

Plugging this into desmos (I know this is cheating), the maximum is at x=10.

Notice that 2nd person gets bigger piece of pie than 1st and so on, until n+1th person gets smaller amount of pie than n-th. Let's naively set up an equation where two consecutive people get equal amounts: first of them gets p of the (remaining) pie, and second (p+0.01)(1-p) of it. p = p - p^2 + 0.01 - 0.01p which yields p = 0.095. It's easy to check that 10th person gets more than 9th (11th) person.

Using Python 3.6:

Here is an Excel solution:

Let’s assume this pie has a total amount of 100. The actual unit doesn’t matter.

In cells A1 through A100, enter numbers 1 through 100. Column A represents n.

In cell B1, enter: =(A1/100)*100

In cell B2, enter: =(A2/100)*(100-SUM($B$1:B1))

Copy cell B2 and paste into cells B3 through B100. Column B represents the amount of pie the corresponding nth person will get.

You will find that at n=10, the amount in cell B10 is the highest at 6.2816. This means the 10th person, or n = 10, gets the most pie.