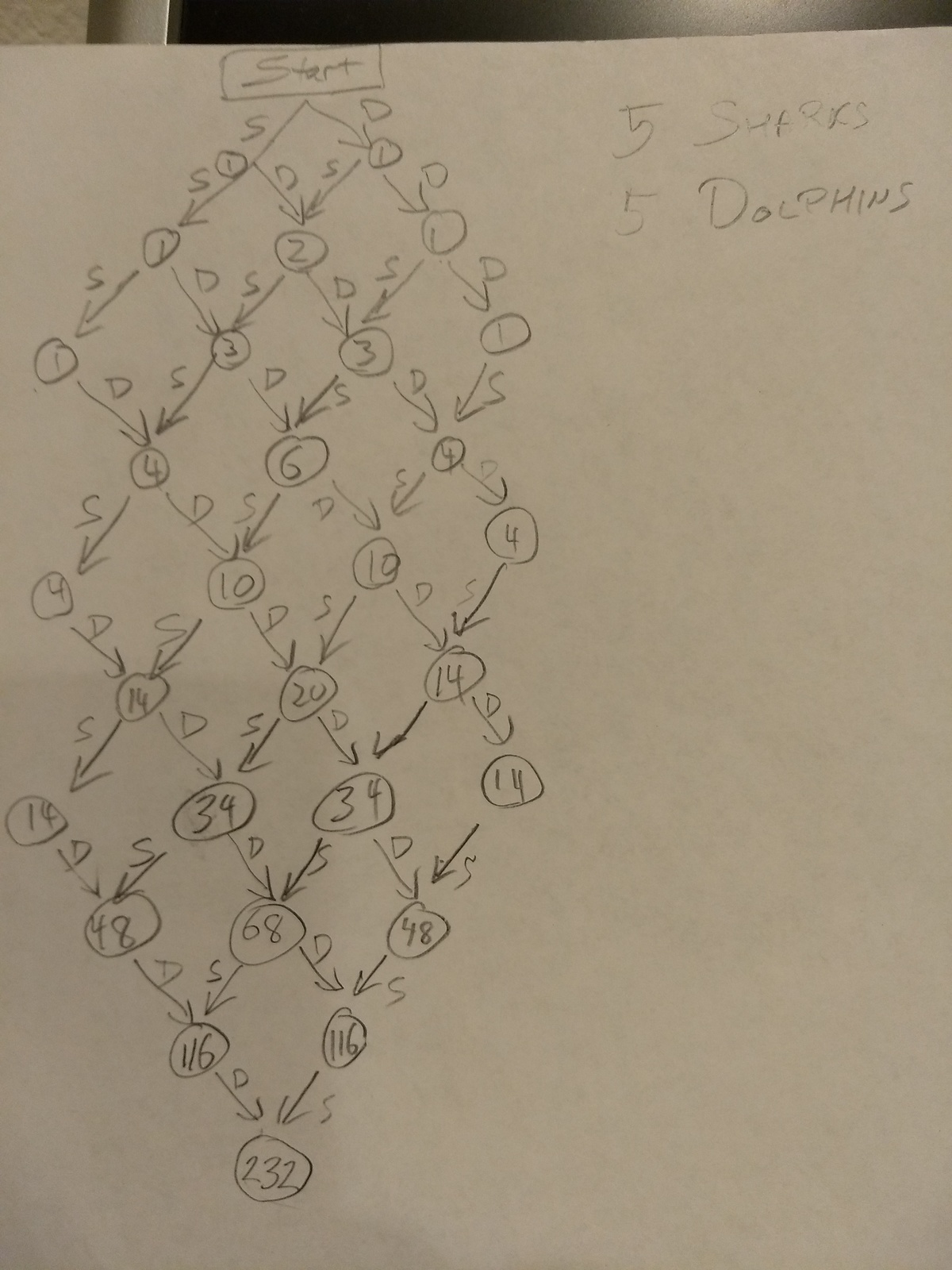
Sharks and dolphins

Probability Level 3

Five indistinguishable sharks and five indistinguishable dolphins decide to go for a swim in a (very large) swimming pool.

They get in the water one at a time, and at no time can either species outnumber the other by more than three.

How many different ways can all ten get in?

For example, one possible way they could enter the pool would be as follows:

S → D → S → D → S → D → S → D → S → D . S \to D \to S \to D \to S \to D \to S \to D \to S \to D.


The answer is 232.

Geoff Pilling by Geoff Pilling , 53, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Puneet Sharma
Oct 17, 2018

2 Helpful 0 Interesting 0 Brilliant 0 Confused
Geoff Pilling
Oct 12, 2018

Here is my thinking. Starting from the top, a shark or dolphin enters the pool one at a time. The circled numbers, are the number of ways they could have reached that particular combination of sharks and dolphins. (e.g. 2 dolphins and 3 sharks)

2 Helpful 0 Interesting 0 Brilliant 0 Confused

Fun problem! I used a similar approach on a 5 by 5 grid, blocking out the verboten nodes and subtracting the number of paths involving those nodes from C ( 10 , 5 ) C(10,5) . Anyway, this OEIS sequence appears to fit the requirements.

Brian Charlesworth - 2 years, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...