Sharks, Dolphins and Whales

The positions of the sharks in the line is immaterial to the problem.

Since there are 3 dolphins and 4 whales, there are $\binom{4+3}{3}$ ways to arrange them (since we don't care about the relative order of the sharks or that of the whales), only one of which will put all 3 dolphins ahead of the whales.

So, the probability is:

$P = \frac{1}{\binom{7}{3}} = \frac{1}{35}$

$1+35 = \boxed{36}$

The total number of arrangements is $\dfrac{12!}{5! 4! 3!}=27720$

Now arrange the dolphins and whales as shown in fig.

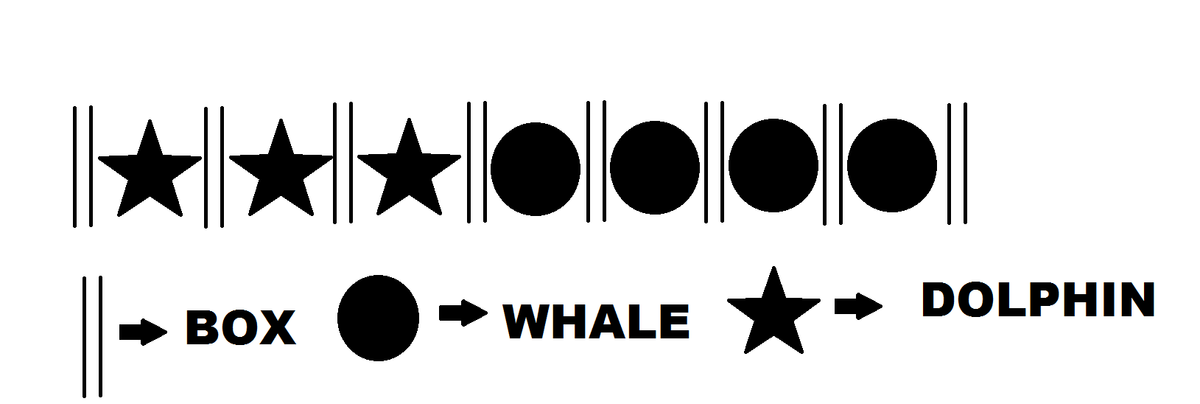
The $5$ sharks can be distributed among the $8$ available boxes

by stars and bars this can be done in

$\dbinom{n+k-1}{n}$ ways where n is the number of objects and k the number of boxes

here $n=5$ and $k=8$ , thus we have $\dbinom{12}{5}=792$ ways

the probability is $\dfrac{792}{27720}=\dfrac{792}{792\times 35}=\dfrac{1}{35}$

thus $a+b=35+1=\boxed{36}$