Shattering Points

Geometry Level 1

Krishna and Satvik are playing a game called 3-Point Shattering , which has the following rules:

Krishna chooses where to place 3 points on a large sheet of paper.
Satvik marks each point either blue or red.
Krishna tries to draw a line such that all the blue points are on one side of it and all the red points are on the other.

Krishna wins if he can do Step 3. Otherwise, Satvik wins. Here are some examples of how Krishna can win:

Notice that Krishna can still win if Satvik marks all the points the same color.

However, if they played a slightly different game, 4-Point Shattering , where Krishna starts by placing 4 points, who has a winning strategy?

Satvik Krishna

9 solutions

Steven Yuan
Feb 9, 2018

No matter how Krishna chooses the four points, Satvik can always label the points in such a way that Krishna can’t shatter them.

If Krishna selects four collinear points, then Satvik can alternate +, -, +, - along the line.
If Krishna selects three collinear points and a point not on the line, then Satvik can assign +s to the endpoints of the line and -s to the rest of the points.
If Krishna selects four points such that they form a convex quadrilateral, then Satvik can assign the points so that going clockwise they are labeled +, -, +, -.
Finally, If Krishna selects four points such that they form a concave quadrilateral, then Satvik can assign the outer triangular portion to + and the inner point to -. (That was the case I missed originally.)

Therefore, Satvik has the winning strategy.

This is pretty cool, isn't it? These things are known as VC dimensions and one of the interesting implications this theory has is to be able to figure out whether a certain kind of datset can be classified using Support Vector Machines.

Agnishom Chattopadhyay - 3 years, 4 months ago

Linear classification in ML was the thing that I immediately thought about, too!

Uros Stojkovic - 3 years, 3 months ago

I think you need to slightly modify the argument by making another case distinction in your last step: Your description only works if the four points form a convex quadrilateral. (Otherwise I also don't quite understand what you mean by "diagonally opposite"). If however three of the four points form a triangle containing the fourth, any choice of assigning two +'s and two -'s to the four points will make it possible for Krishna to win. In this case you want to mark the vertices of the triangle with one color and the point in its interior with the other, which provides Satvik with a winning strategy.

Jonas R - 3 years, 4 months ago

I agree with this observation.

Bryan Bischof - 3 years, 3 months ago

Yeah, I didn’t think about the concave quadrilateral case until you brought it up. I’ve edited my solution to include that case. Thanks!

Steven Yuan - 3 years, 3 months ago

Wait Wait your question was : "However, if they played a slightly different game, 4-Point Shattering, where Krishna starts by placing 4 points, who has a winning strategy?" Krishna starts by placing 4 points so Satvik can't draw a line then &Krishna wins! the four-point game.

Antariksha Mitra - 3 years, 3 months ago

Satvik chooses the colors of points, Krishna drawes the line

Андрей Фасалов - 3 years, 3 months ago

Krishna starts by placing 4 points , Satvik assigns red/blue colour to them and then Krishna draws the line!

Toshit Jain - 3 years, 3 months ago

I just simply saw it as making sure your coloured points are opposite pairs.

Matthew Hellwig - 3 years, 3 months ago

Krishna always wins, because nowhere is stated there must be a straight line.

Hilberto Silva - 3 years, 3 months ago

By definition, all lines are straight. If the problem said curves instead of lines, then Krishna will always win, as you stated.

Steven Yuan - 3 years, 3 months ago

What if in case of 3 points scattering the points are collinear with point of different colour in the middle?

Soham Abhishek - 3 years, 3 months ago

Then, Satvik wins, as Krishna won't be able to draw his line. There are many win conditions for both of them with just 3 points, but if it's 4, Satvik always wins..

Matthew Hellwig - 3 years, 3 months ago

What if Krishna puts 4 points without touching the border of the paper in a square shape formation?

Lys Lol - 3 years, 3 months ago

All Satvik has to do then is colour opposite pairs.

Matthew Hellwig - 3 years, 3 months ago

it doesn't say the line has to be straight !

Jim Reeves - 2 years ago

It is standard in the conventional mathematical literature to assume that "line" refers to "straight line" unless mentioned otherwise.

Agnishom Chattopadhyay - 2 years ago

Timofey Urbanovich
Feb 12, 2018

Let's look at сonvex hull of Krishna's points. If points are distinct we have these possibilities: 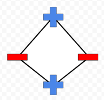Quadrilateral 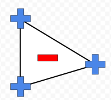Triangle with fourth point inside it 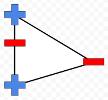Triangle with fourth point on its side 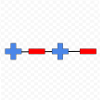Segment Segment In each of this cases there is no line dividing blue points from red ones.

Its worth noting that 3 collinear points loses even in the original 3-point game.

Marcelo Cantos - 3 years, 3 months ago

John Smith
Feb 11, 2018

Sitvak can place blue and red dots so that they form 2 crossing segments. In that case, Kirshna cannot find any solution.

Not working if 3 dots form a triangle, and inside it the fourth dot are placed. http://ibb.co/igxLT7 In this case you need to choose 3 points as red and 1 as blue.

Андрей Фасалов - 3 years, 3 months ago

He doesn't place them, he only colours them.

Matthew Hellwig - 3 years, 3 months ago

Problem did not state it had to be a straight line.

Dinshaw Burjorjee - 3 years, 3 months ago

Mark Hennings
Feb 12, 2018

If any three points are collinear, colour the middle one differently to the other two.

If the four points form a convex quadrilateral, colour the diagonally opposite vertices the same (with a different colour for each diagonal).

If the four points do not form a convex quadrilateral, so that one point lies inside the triangle formed by the other three, paint the interior point one colour and the other three points the other colour.

Satvik wins.

Roman Sologub
Feb 12, 2018

Erm, Ok, I'm Krishna. I put points at: (0,0) (0,1) (1,-1) (-1,-1)

Go on, Satvik, invent something.

Looks like the right answer is wrong.

Moderator note:

As pointed out by Timothy in the comments, this coloring is impossible to split with a single straight line:

Satvik marks (0,0) red and the rest blue.

Timothy Watson - 3 years, 3 months ago

Timothy is correct. The right answer is right.

Markus Pfaff - 3 years, 3 months ago

All Satvik has to do to win is create two crossing lines with the points, which is always possible. In this case, if (0,0) and (1,-1) are red and (-1,1) and (1,0) and blue, Krishna cannot win.

Matthew King - 3 years, 3 months ago

Why does Satvik mark (-1,1) and (1,0) blue yet Krishna didnt choose those points?

A Former Brilliant Member - 3 years, 3 months ago

Well I just draw the line y=3x+1/2 if I am Krishna.

CHIN KEE HAW - 3 years, 3 months ago

Ah, my bad. For some reason thought he had to make 2 points red and 2 points blue.

Roman Sologub - 3 years, 3 months ago

Kramers Kronig
Feb 14, 2018

Roman: (0,0) is red, all other blue. Satvik wins.

If you count that Krishna wins in the 3 dots case if all the three points are in the whatever neg or pos sign, then we call this case all three points, namely all three dots out of three, so it is 3/3=1 which is the score Krishna waits. The other two cases are neg dot and two pos dots which are divisible in the case 2/3or1/3,but anyhow a remainder of 1/3 breaks Krishna's win. In the four dots case Krishna wins if four dots are in the one side of the line that is drawn. So for example if we have total of four dots neg or pos together, Krishna wins if she scores 4/4=1, which is the winning probability. In all other cases that are two neg or pos and one neg or pos dots the possibility for Krishna is about 1/2 twice and 1/4 twice so the wining probability in this case is 1/5 which is smaller than 1/3. So in the second case Satvik can have a better chance than before from Krishna.

Orla Koci - 3 years, 3 months ago

Jerome Mourey
Feb 13, 2018

The 4-point version of the game mage me think about the XOR problem in machine learning. We cannot simulate the XOR function with a linear approximation. see more about the xor problem

Whatever position Krishna choose we can find a linear transformation which move each point to a corner of a square. (except if she put all the point on a line but just alternate color)
We only have the alternate the color of connected corner. Two connected corner must have a different color.
It is now impossible to draw a line which separate the two color.

Sahit Dodda
Feb 12, 2018

If Satwik simply alternates them he wins. The only way Krishna has no chance of winning in 3 points is if he puts them in a straight line, but no matter what, the alterations prevent any win in 4+ points.

Cen Liang
Feb 12, 2018

There are three cases in Step One:Two point collinear Three point collinear and Four point collinear. In whichever case, Satvik can beat Krishna.

Shattering Points

9 solutions

Moderator note:

0 pending reports