Shell Gravity

Classical Mechanics Level 3

There is a shell in the shape of a half sphere of radius 1 1 centered on the origin (defined for z ≥ 0 ) z \geq 0) . It has a uniform area mass density of 1 1 . The universal gravitational constant is G G .

There is a test point at the origin.

If the absolute value of the gravitational field strength at the test point is α \alpha , give your answer as α G \large{\frac{\alpha}{G}} .

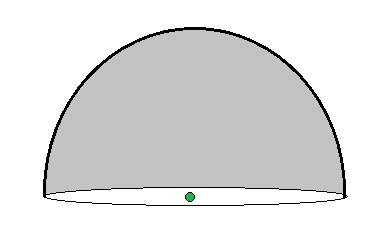
Note: There is no ambient gravity


The answer is 3.14159.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Otto Bretscher
Dec 21, 2018

The gravitational field at the origin will be vertical, by symmetry. The z z -component is ∫ ∫ S z d S = z ‾ ( area of S ) = 1 2 × 2 π = π ≈ 3.1416 \int\int_S z \ dS=\overline{z}(\text{area of } S)=\frac{1}{2}\times 2\pi=\pi\approx \boxed{3.1416} .

0 Helpful 2 Interesting 1 Brilliant 0 Confused

The hemisphere is symmetrical around the vertical axis. Therefore, only fraction part of the gravitational force that is vertical is significant. The radius is given as being 1. The problem is simplified by setting the value of G to 1 to avoid the division at the end. The integration is 2 π ∫ 0 π 2 cos ⁡ sin ⁡ ( θ ) d θ . 2 \pi \int_0^{\frac{\pi }{2}} \cos \sin (\theta ) \, d\theta. (which can be integrated easily by substitution of variables) is π \pi .

0 Helpful 1 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...