Shell it out
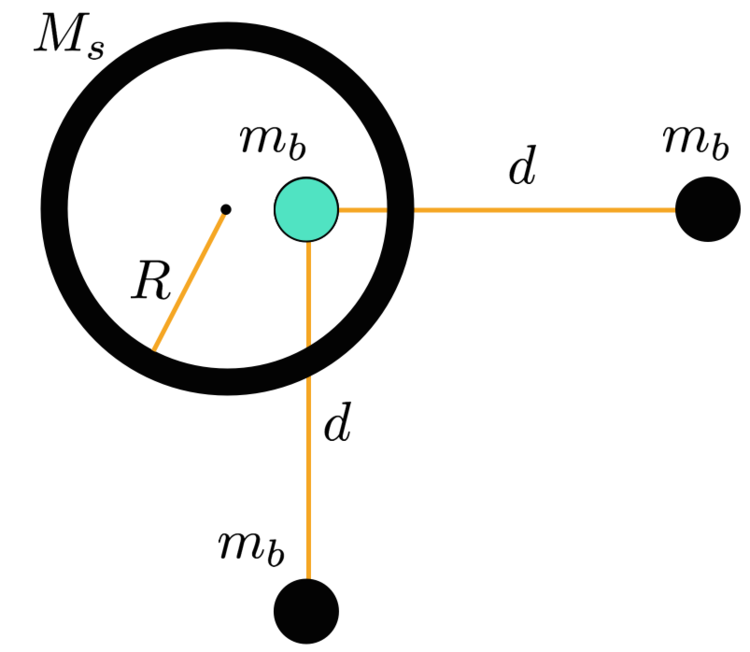 A green sphere of mass
m
b
is placed inside a spherical shell of radius
R
and mass
M
s
. Two spheres identical in mass to the green sphere are placed a distance
d
to the right and to the bottom, respectively, of it. What is the magnitude of the gravitational force on the green sphere?
A green sphere of mass
m
b
is placed inside a spherical shell of radius
R
and mass
M
s
. Two spheres identical in mass to the green sphere are placed a distance
d
to the right and to the bottom, respectively, of it. What is the magnitude of the gravitational force on the green sphere?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since gravitational force on a point mass inside a uniform spherical shell is zero so we have net force on the mass as d 2 2 G m b 2 .
Gravitational force on a point mass inside a uniform spherical shell is zero.
Gravitational force between A and B = d 2 G m b 2 \overset{\^}{i}
Gravitational force between A and C = d 2 G m b 2 \overset{\^}{j}
Taking vector sum, magnitude of total gravitational force experienced by the green Sphere = d 2 2 G m b 2