Shell Potential Energy
Consider the half spherical shell:
x 2 + y 2 + z 2 = 1 z ≥ 0
The shell has area mass density ρ = ( x y z ) 2 . The ambient gravitational acceleration is 1 0 in the negative z direction.
Determine the gravitational potential energy of the shell relative to the plane z = 0 .
The answer is 0.3272.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Karan Chatrath
i was solving this question through this method but not able to obtain correct answer. Can you help?? Here is my solution.

Log in to reply
Your area element definition does not account for the curvature of the sphere.
Log in to reply
@Karan Chatrath okay ! . I was upgrading this question and making a new question like this only but will note hemi-sphere, it will be hemi-epllisoid. But I am unable to parameterise that ellipsoid . Help?
F u n P r o b l e m
x
=
cos
α
sin
β
y
=
sin
α
sin
β
z
=
cos
β
0
≤
α
≤
2
π
0
≤
β
≤
π
/
2
d
S
=
sin
β
d
α
d
β
d
m
=
ρ
d
S
Consider
G
as Gravitational potential energy.
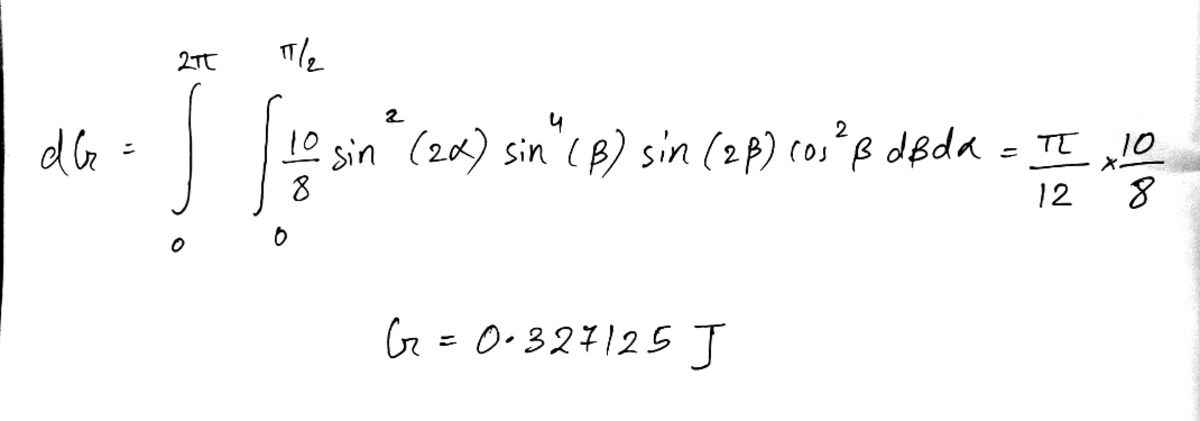
I think the answer you have obtained is incorrect. For the following few reasons:
- The integrand misses a factor of 10
- 1 2 π does not evaluate to 0.32. It instead evaluates to approximately 0.26.
Please review your work.
Log in to reply
@Karan Chatrath YEAH!, thanks for the correction. Speed thrills but kills.
Consider the given scenario which is analysed in spherical coordinates. Any point on the surface of the sphere is:
x = sin θ cos ϕ y = sin θ sin ϕ z = cos θ
A surface area element is:
d S = sin θ d θ d ϕ
Mass per unit area is:
ρ = ( x y z ) 2 = sin 4 θ cos 2 θ sin 2 ϕ cos 2 ϕ
Therefore the mass of an elementary surface area is:
d m = ρ d S = sin 5 θ cos 2 θ sin 2 ϕ cos 2 ϕ d θ d ϕ
The potential energy due to this mass is:
d V = d m g z
d V = 1 0 sin 5 θ cos 3 θ sin 2 ϕ cos 2 ϕ d θ d ϕ
V = ∫ 0 π / 2 ∫ 0 2 π 1 0 sin 5 θ cos 3 θ sin 2 ϕ cos 2 ϕ d θ d ϕ
Since the limits of integration are constant:
V = 1 0 ( ∫ 0 π / 2 sin 5 θ cos 3 θ d θ ) ( ∫ 0 2 π sin 2 ϕ cos 2 ϕ d ϕ ) ⟹ V = 1 0 ( ∫ 0 π / 2 sin 5 θ cos 3 θ d θ ) ( 4 ∫ 0 π / 2 sin 2 ϕ cos 2 ϕ d ϕ )
Using the following formula:
∫ 0 π / 2 sin m θ cos n θ d θ = 2 Γ ( 2 m + n + 2 ) Γ ( 2 m + 1 ) Γ ( 2 n + 1 )
Where Γ ( n ) is the Gamma function. Applying the above gives:
V = 4 0 ( 2 Γ ( 2 5 + 3 + 2 ) Γ ( 2 5 + 1 ) Γ ( 2 3 + 1 ) ) ( 2 Γ ( 2 2 + 2 + 2 ) Γ ( 2 2 + 1 ) Γ ( 2 2 + 1 ) )
⟹ V = 4 0 ( 2 Γ ( 5 ) Γ ( 3 ) Γ ( 2 ) ) ( 2 Γ ( 3 ) Γ ( 2 3 ) Γ ( 2 3 ) )
Using the facts that for integers Γ ( n + 1 ) = n ! , and in general Γ ( n + 1 ) = n Γ ( n ) and also the fact that Γ ( 2 1 ) = π . Applying these results and simplifying gives the answer:
V = 4 8 5 π ≈ 0 . 3 2 7 2 5