Shhhh! Don't give me the hint
For positive real numbers a , b , c , d , find the minimum value of the following expression:
( a + b + c + d ) ( a 2 5 + b 3 6 + c 8 1 + d 1 4 4 ) .
The answer is 1024.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Equality case?
Log in to reply
a = 5 , b = 6 , c = 9 , d = 1 2 ... I think you're commenting the same whenever you want to troll me or Dinesh or anyone else :P
Ya i learnt it in elementary number THEORY a very nice book
OMG I GOT ALL THE STEPS CORRECT BUT I FORGOT THAT WE HAD TO SQUARE THE 32 IM SO FRUSTRATED
What if we use rearrangement inequality?
Occurs at 100, 20 and 100/17, at least.
Can Also be done by AM-HM
5 + 6 + 9 + 1 2 5 ∗ 5 a + 6 ∗ 6 b + 9 ∗ 8 1 c + 1 2 ∗ 1 2 d ≥ 5 ∗ a 5 + 6 ∗ b 6 + 9 ∗ c 9 + 1 2 ∗ d 1 2 5 + 6 + 9 + 1 2
Equality occurs when all terms are equal
AM-HM inequality only works for positive numbers, question states for all real numbers.
I suppose Weighted A.M-H.M Inequality is derivative of C-S Inequality...
Nice solution. For those wondering, there are many values of a, b, c, d that will make the expression equal 1024, so long as they satisfy the equations a/5 = b/6 = c/9 = d/12.
Sorry....But it is not always the case that equality occurs when variables are equal...
Can it be done by rearrangememt inequality?
i used titu's lemma .direct answer
can you explain it please
So did I! 25 = 5^2 36 = 6^2 81 = 9^2 144 = 12^2 According to Titu's lemma, 5^2/a + 6^2/b + 9^2/c + 12^2/d is greater than or equal to (5+6+9+12)^2/(a+b+c+d) = 1024/(a+b+c+d) Minimum exists when there is equality. a + b + c in the numerator and denominator cancel out, leaving us with 1024.
Titu's lemma is just a simple modified version of Cauchy Schwarz inequality I think.
why are we not using am-gm inequality? is it the reason that it will bring the minimum value sq. root of 3240 which is not an integer.....but shouldn't that be the least value??
It is also possible to find the minimum via the AM-GM. You can in fact multiply and get 16 terms. 4 of them are constant and the other 12 can be grouped in six pairs of the kind 3 6 b a + 2 5 a b You then apply the AM >= GM on each of this pair (for istance you get 3 6 b a + 2 5 a b ≥ 6 0 on the pair considered above and repeat same argument for the other five pairs ) and get the upper bound 1024 (that is indeed attained).
So this problem can be solved by C-S, AM-GM, AM-HM. Can anyone find a proof involving QM-AM inequality????
Also I want to note that even with C-S(or Titu's lemma) the terms a , b , c , d must be positive (at least at first glance) in order to consider the square roots a , b , c and d . So if we want to get a proof for a , b , c , d non zero reals we must find a fitting argument (is not enough to just throw in the fact that the C-S inequality works for every real numbers).
If any body saw squares and randomly tried their root as input , Its meeee !!! Got lucky
Okkk.......
Ahahahaha! BTW Great intuition!
I have used cauchy- schwarz inequality to solve this question.
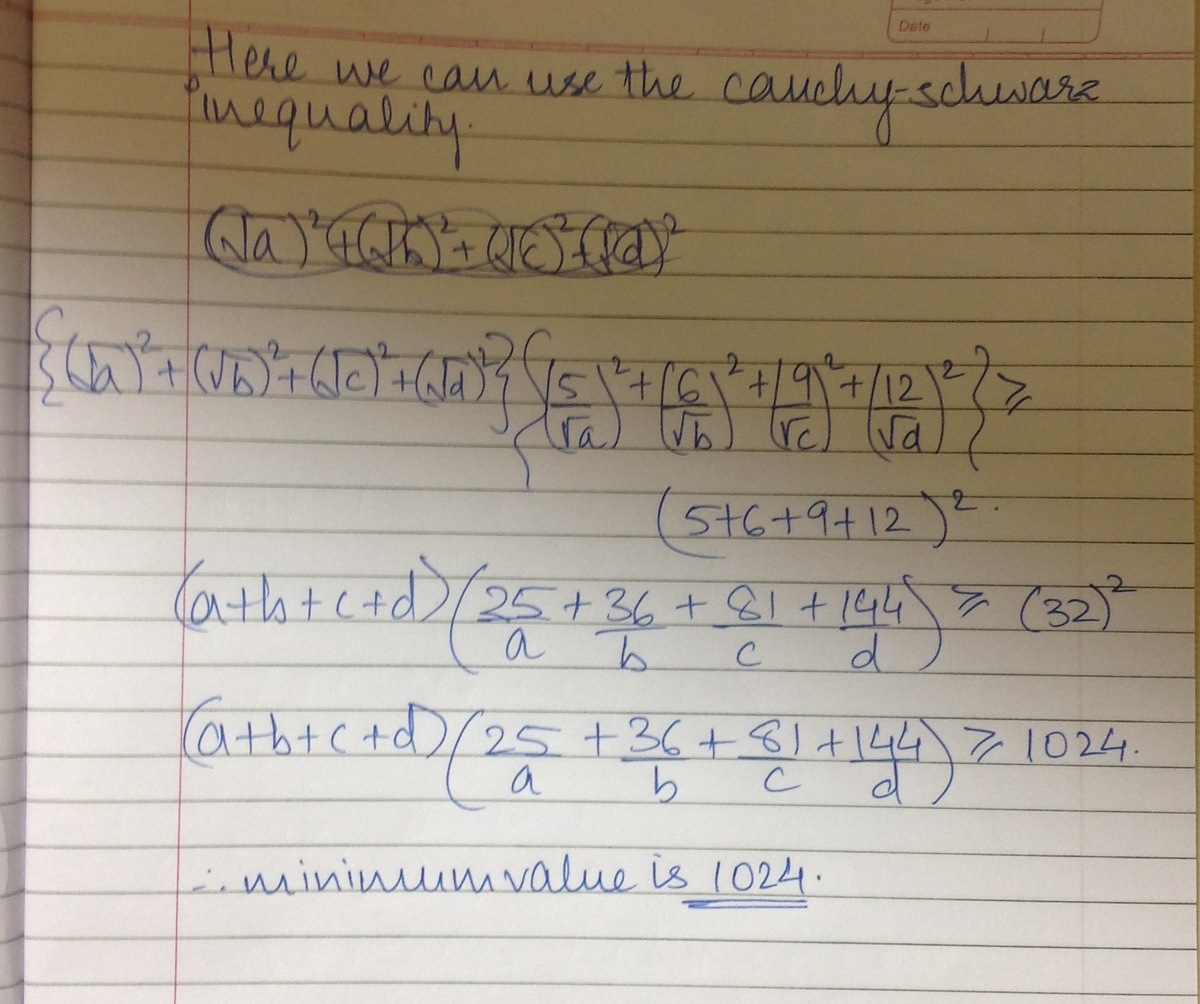
Simply apply Cauchy-Schwarz on
( a 5 , b 6 , c 9 , d 1 2 ) and ( a , b , c , d ) .
Then we have ( ∑ a a k ) 2 ≤ ( ∑ a k 2 ) ( ∑ a ) , so ( 5 + 6 + 9 + 1 2 ) 2 ≤ ( a + b + c + d ) ( a 2 5 + b 3 6 + c 8 1 + d 1 2 ) .
Thus, the answer is 3 2 2 = 1 0 2 4 .
The equality occurs where a 5 = b 6 = c 9 = d 1 2 .