Shifting Circular Heart
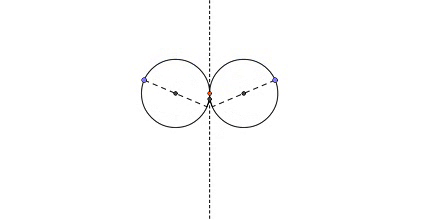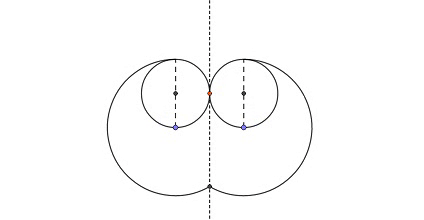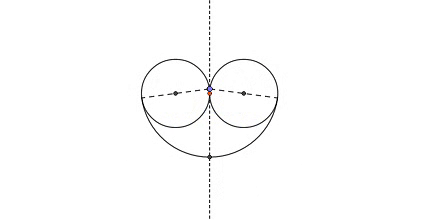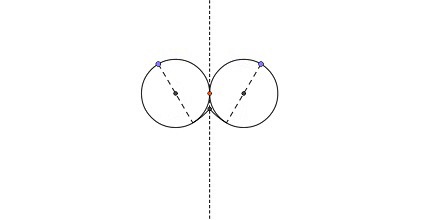
Two unit circles are tangential to each other at the orange point on the dashed line. The two blue points circling on their respective circumferences both extend the circular arcs of radius 2 toward their intersection point.
What is the maximum distance between the orange tangential point and the intersection point of the two arcs?
Round your answer to the nearest thousandths digit.
The answer is 2.828.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Pythagorean Theorem
If each circular arc is tangential to its respective circle, then the centre of the arc must be on the opposite side of the circle from their tangential point, because the radius of the arc is equal to the diameter of the circle.
With this, we know that the maximum distance from the centre of a circle to any point on its respective arc is equal to the radius of a circle ( r ) plus the radius of an arc ( R ).
r + R = 3
3 is then equal to the maximum length of a hypotenuse of a right triangle; formed from the centre of a circle, the tangent of the two circles, and the intersection of the two arcs.
Using the Pythagorean Theorem, we can determine the maximum length ( m ) between the tangent of the two circles and the intersection of the two arcs.
3 2 = 1 2 + m 2
3 2 − 1 2 = 8 = 2 . 8 2 8