Shine bright like a white star
 Given the regular octagon of side length 10 with eight equilateral triangles inside, calculate the white area to 3 decimal places.
Given the regular octagon of side length 10 with eight equilateral triangles inside, calculate the white area to 3 decimal places.
The answer is 136.433.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Same method. This problem when you posted first time , I think you made mistake in calculating areas of equilateral triangle.Hence I was unable to get this question but now I got.☺☺☺
well done
Nice way without using general formula for area of a regular polygon
The area of any regular polygon is given by: 4 1 n L 2 cot n 1 8 0 ° where n is the number of sides such that n > 2, and L is length of each side.
All we need to do is to subtract the area of the octagon by eight of the areas of the equilateral triangles.
4 1 8 ( 1 0 ) 2 cot 8 1 8 0 ° − 8 [ 4 1 3 ( 1 0 ) 2 cot 3 1 8 0 ° ] ⇒ 2 0 0 cot 2 2 . 5 ° − 6 0 0 cot 6 0 ° ⇒ ≈ 1 3 6 . 4 3 3
Moderator note:
Wonderful shortcut! Your solution can certainly generalize the result. Bonus question: Can you prove the formula for the area of a regular n -gon with side length L to be 4 1 n L 2 cot ( L 1 8 0 ∘ ) ?
i used same method..
Wow. I'm impressed. Thank you for this.
your method is so good :)
I used this procedure
I think the cotangent term should have n in the denominator, not L. I did it the same way, and you plugged in 8 anyway, so maybe it's just a typo?
Log in to reply
You are right, it's a typo. I apologize. Thank you for correcting me. ☺👏
Area of octagon is A=2(1+2)a^2 which is equal to 482.842 when a=10.
Area of equilateral triangle is A=(3/4)a^2 which is equal to 43.301 when a=10.
There are total 8 such triangle so total area of all triangle is 43.301*8=346.408
So area of white place = Area of octagon- area of all triangle = 482.842-346.301 = 136.541
your method is easy, no calculator is required.....
Divide the whole thing into eight triangles. The white area is going to be eight times the big triangle (one piece of the octagon) minus the smaller equilateral triangle.
The pinnacle of the big triangle = 45 degrees (360/8), which means that the base of this isosceles has two angles of 67.5 degrees. By simple trigonometry, we get that the area of each triangle is 25tan67.5.
Similarly for the equilateral triangle, the area is 25tan60 (or 25rt3).
Subtracting and multiplying by 8 makes 136.432551.
Using the formula of A=(1/2)aP where A is area, a is the apothem length and P is the perimeter, we find that the apothem is the distance from center to one of it's sides which happens to be the length of one side + 2 of the 5sqrt2, 5sqrt2, 10 leg triangles (a bit confusing to see without a drawing). Therefore, the apothem is (10+10sqrt2)/2 or 5+5sqrt2.
A=(1/2)x5+5sqrt2)(8x10)=200+200sqrt2.
The equilateral triangles have an area of 25sqrt 3 (bh/2=10x5sqrt3/2).
Multiplying this by 8 and subtracting form the area of the octagon yields the area of the white space inside. 200+200sqrt2-(8x25sqrt3)=200+200sqrt2-200sqrt3.
Factoring out 200 yields 200(1+sqrt2-sqrt3) which, by using a calculator of course, yields 136.43255 by 3 decimal places yields 136.433.
Since the triangles are equilateral, the area of one of them would be 1/2 10 *10 sin(60 degrees). This is so since we know that all sides are of the same length for an equilateral triangle and that its interior angles are identical as well. Multiply this value by eight to obtain the total shaded area. Find the area of the octagon using a^2 2 (1+2^(1/2)) where a is the value of one side of the octagon. Find the difference between the two values you just obtained to get the answer. I wouldn't say it's the best solution, but at least it works well for me given that I'm not that advanced into Mathematics.
\frac{(8 \times 10 \times 5 \times (1+ \sqrt{2} - \sqrt{3}))} {2}
area of 8 equilaterals=8 * 5 sqr(3) * 5 = 200 sqr(3) remaining area (the star) = 2(1+sqr(2)) 10 10 - 200 sqr(3) = 136.432
As triangles are equilateral and we have one of its sides, the area of one is given by 4 a 2 3 = 4 1 0 2 3 = 2 5 3 ⇒ all the black area is 8 ( 2 5 3 ) = 2 0 0 3
Also is necessary calculate the octagon area. For that, I constructed a square outside of the octagon. Then we get four triangles 4 5 ° − 9 0 ° − 4 5 ° (as the picture shows).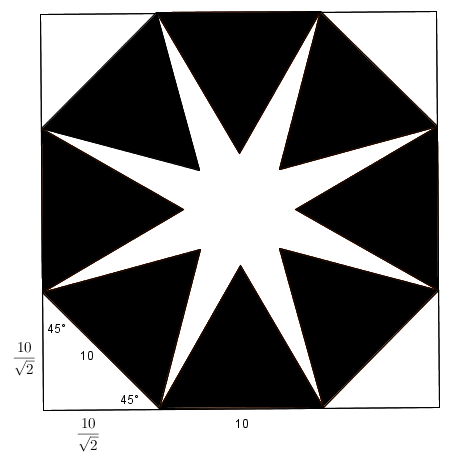
Using pythagorean theorem we get its sides:
s 2 + s 2 = 1 0 2
2 s 2 = 1 0 2
s = 2 1 0 2 = 2 1 0
Then, the octagon area is square area − four triangles area
square area = ( 2 1 0 + 2 1 0 + 1 0 ) 2 = ( 2 2 0 + 1 0 ) 2 = 3 0 0 + 2 0 0 2
four triangles area = 2 ( 2 1 0 ) 2 = 1 0 0
So the octagon area is 3 0 0 + 2 0 0 2 − 1 0 0 = 2 0 0 + 2 0 0 2
Finally, the white area is 2 0 0 + 2 0 0 2 − 2 0 0 3 ≈ 1 3 6 . 4 3 3