Shiny Sternenhimmel

Geometry Level 4

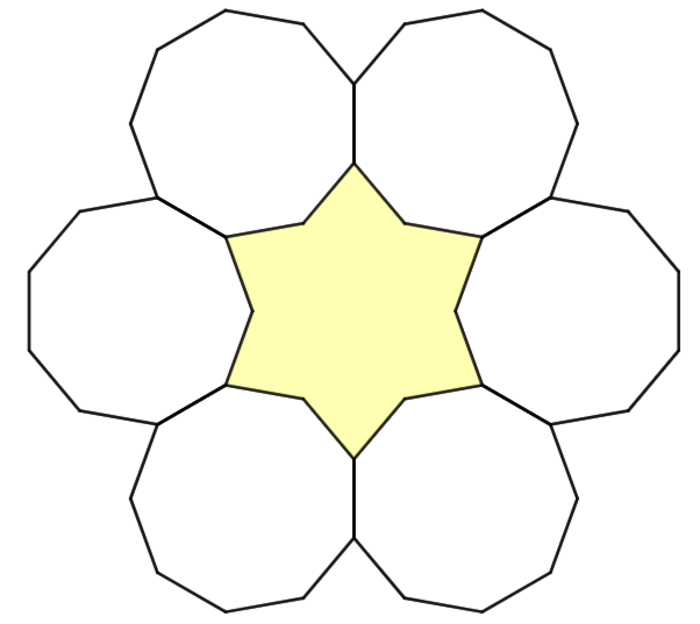
As shown above, the yellow polygon is surrounded by six unit regular nonagons. If the area of the yellow polygon can be expressed as

A sin ⁡ π 9 + B sin ⁡ π 3 A\sin\dfrac{\pi}{9} + B\sin\dfrac{\pi}{3}

where A A and B B are integers, input the product A B AB as your answer.


The answer is 36.

Michael Huang by Michael Huang , 29, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

David Vreken
Jan 27, 2021

The yellow polygon can be divided into 12 12 unit equilateral triangles and 6 6 unit rhombi (with angles of π 9 \cfrac{\pi}{9} and 8 π 9 \cfrac{8\pi}{9} ):

Since each equilateral triangle has an area of 1 2 sin ⁡ π 3 \cfrac{1}{2}\sin \cfrac{\pi}{3} and each rhombi has an area of 2 ⋅ 1 2 ⋅ 1 ⋅ 1 ⋅ sin ⁡ π 9 = sin ⁡ π 9 2 \cdot \cfrac{1}{2} \cdot 1 \cdot 1 \cdot \sin \cfrac{\pi}{9} = \sin \cfrac{\pi}{9} , the total area is 12 ⋅ 1 2 sin ⁡ π 9 + 6 sin ⁡ π 3 12 \cdot \cfrac{1}{2}\sin \cfrac{\pi}{9} + 6 \sin \cfrac{\pi}{3} or:

6 sin ⁡ π 9 + 6 sin ⁡ π 3 6 \sin \cfrac{\pi}{9} + 6 \sin \cfrac{\pi}{3}

Therefore, A = B = 6 A = B = 6 and A B = 36 AB = \boxed{36} .

4 Helpful 3 Interesting 7 Brilliant 0 Confused

This is indeed a brilliant solution! Can't stop looking at it! Congratulations, sir!

P.S.: Rhombi sounds funny.

Veselin Dimov - 4 months, 2 weeks ago

But is there only one solution of ( A , B ) (A,B) ?

Pi Han Goh - 4 months, 2 weeks ago

Log in to reply

Yep :-) 

1
2
3
4
5
6
7
 
import math
G = 6.0 * (math.sin(math.pi / 9) + math.sin(math.pi / 3))
for A in range(1, int(1.0 * G / math.sin(math.pi / 9)) + 1):
    for B in range(1, int(1.0 * G / math.sin(math.pi / 3)) + 1):
        V = A * math.sin(math.pi / 9) + B * math.sin(math.pi / 3)
        if math.isclose(V, G):
            print(G, V, A, B)

David Vreken - 4 months, 2 weeks ago

Log in to reply

Oh, I guess this only proves one solution for positive integers...

David Vreken - 4 months, 2 weeks ago
Chew-Seong Cheong
Jan 27, 2021

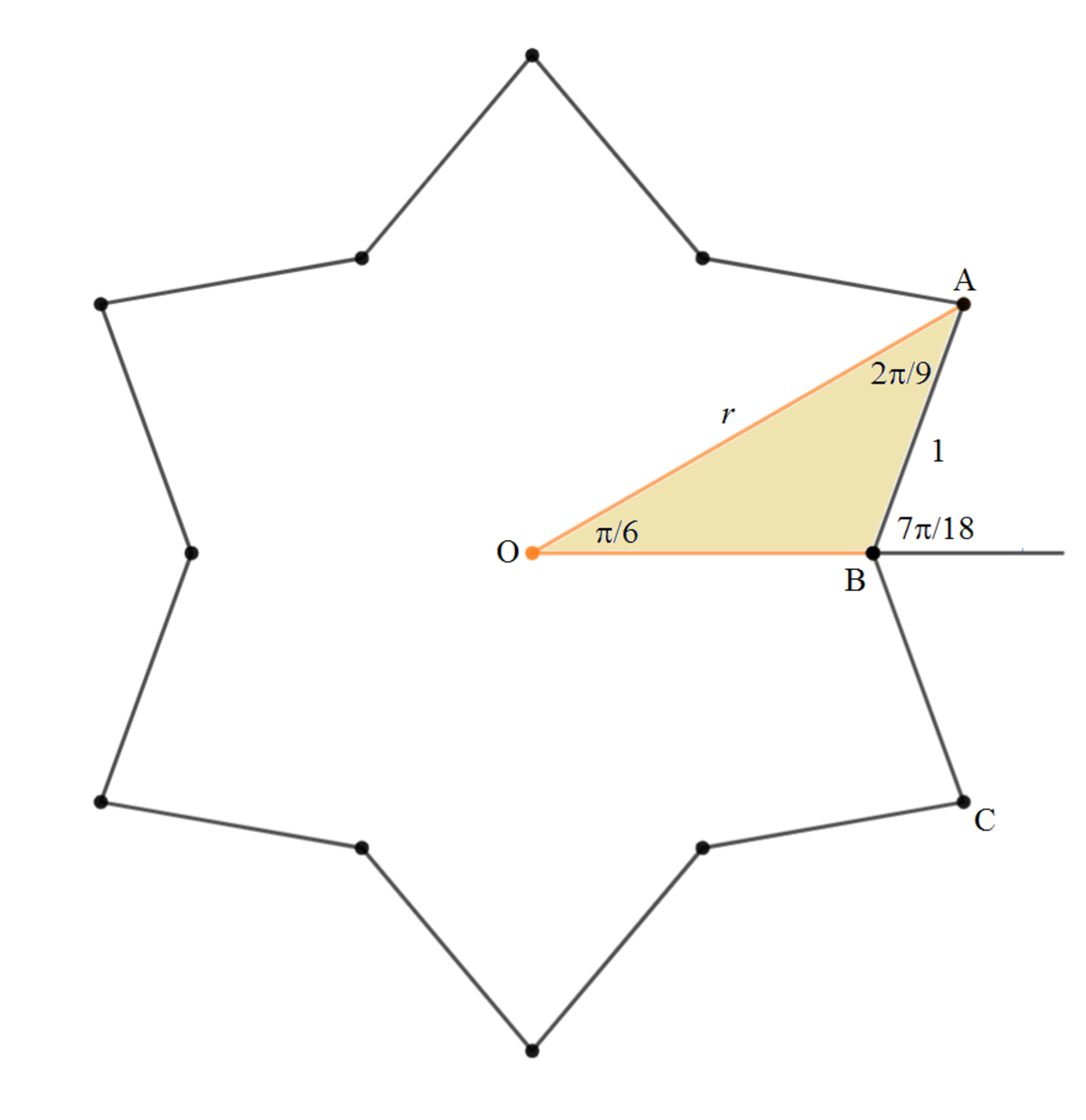
The yellow polygon is a 12-sided polygon with unit side length symmetrical about its center O O . The area of the yellow polygon is 12 12 times that of △ O A B \triangle OAB . The central angle ∠ A O B = 2 π 12 = π 6 \angle AOB = \dfrac {2\pi}{12} = \dfrac \pi 6 . A B AB and B C BC are sides of a unit regular nonagon. Therefore ∠ A B C = 9 − 2 9 π = 7 π 9 \angle ABC = \dfrac {9-2}9 \pi = \dfrac {7\pi}9 and the supplementary angle of ∠ A B O = ∠ A B C 2 = 7 π 18 \angle ABO = \dfrac {\angle ABC}2 = \dfrac {7\pi}{18} and ∠ O A B = 7 π 18 − π 6 = 2 π 9 \angle OAB = \dfrac {7\pi}{18}-\dfrac \pi 6 = \dfrac {2\pi}9 . Let O A = r OA = r . By sine rule ,

O A A B = sin ⁡ ∠ A B O sin ⁡ ∠ A O B r 1 = sin ⁡ ( π − 7 π 18 ) sin ⁡ π 6 Note that sin ⁡ ( π − θ ) = sin ⁡ θ ⟹ r = 2 sin ⁡ 7 π 18 \begin{aligned} \frac {OA}{AB} & = \frac {\sin \angle ABO}{\sin \angle AOB} \\ \frac r1 & = \frac {\sin \left(\pi - \frac {7\pi}{18}\right)}{\sin \frac \pi 6} & \small \blue{\text{Note that }\sin (\pi -\theta) = \sin \theta} \\ \implies r & = 2 \sin \frac {7\pi}{18} \end{aligned}

The area of the yellow polygon,

A = 12 ⋅ O A ⋅ A B ⋅ sin ⁡ ∠ O A B 2 = 12 ⋅ 2 sin ⁡ 7 π 18 ⋅ 1 ⋅ sin ⁡ 2 π 9 2 = 12 sin ⁡ 7 π 18 sin ⁡ 2 π 9 Note that cos ⁡ ( A − B ) − cos ⁡ ( A + B ) = 2 sin ⁡ A sin ⁡ B = 6 ( cos ⁡ π 6 − cos ⁡ 11 π 18 ) and cos ⁡ ( π − θ ) = − cos ⁡ θ = 6 ( cos ⁡ π 6 + cos ⁡ 7 π 18 ) also cos ⁡ θ = sin ⁡ ( π 2 − θ ) = 6 ( sin ⁡ π 3 + sin ⁡ π 9 ) \begin{aligned} A & = 12 \cdot \frac {OA \cdot AB \cdot \sin \angle OAB}2 \\ & = 12 \cdot \frac {2 \sin \frac {7\pi}{18} \cdot 1 \cdot \sin \frac {2\pi}9}2 \\ & = 12 \sin \frac {7\pi}{18} \sin \frac {2\pi}9 & \small \blue{\text{Note that }\cos(A-B)-\cos (A+B) = 2\sin A \sin B} \\ & = 6 \left(\cos \frac \pi 6 - \blue{\cos \frac {11\pi}{18}}\right) & \small \blue{\text{and }\cos (\pi - \theta) = - \cos \theta} \\ & = 6 \left(\cos \frac \pi 6 + \blue{\cos \frac {7\pi}{18}}\right) & \small \blue{\text{also }\cos \theta = \sin \left(\frac \pi 2 - \theta\right)} \\ & = 6 \left(\sin \frac \pi 3 + \sin \frac \pi 9 \right) \end{aligned}

Therefore A B = 6 ⋅ 6 = 36 AB = 6 \cdot 6 = \boxed{36} .

3 Helpful 2 Interesting 3 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...