Field Motion

LET the charged particle be at distance "x" from the center of the ring , and consider a "dl" lenght of the ring the charge of the "dl" segment $dQ=\frac { Q }{ 2\pi a } dl$ the force on smaller charge due to the "dl" lenght $dF=\frac { -Qqdl }{ 4\pi \epsilon(2\pi a)({ x }^{ 2 }+{ a }^{ 2 }) }$ but the $dFSin\theta$ component will cancel out and only $dFCos\theta$ will remain $dF=\frac { -Qqdl }{ 4\pi \epsilon(2\pi a)({ x }^{ 2 }+{ a }^{ 2 }) } \times Cos\theta =\frac { -Qqdl }{ 4\pi \epsilon(2\pi a)({ x }^{ 2 }+{ a }^{ 2 }) } \times \frac { x }{ \sqrt { { x }^{ 2 }+{ a }^{ 2 } } }$ integrating we will obtain $F=\frac { -Qqx }{ 4\pi \epsilon({ x }^{ 2 }+{ a }^{ 2 })^{3/2} }$ taling a common $\frac { -Qqx }{ 4\pi { a }^{ 3 }\epsilon { (\frac { { x }^{ 2 } }{ { a }^{ 2 } } +1) }^{ 3/2 } }$ $\frac { -Qqx }{ 4\pi { a }^{ 3 }\epsilon }$ $acceleration=\frac { -Qqx }{ 4\pi m{ a }^{ 3 }\epsilon }$ ${ (\frac { 2\pi }{ T } ) }^{ 2 }=\frac { Qq }{ 4\pi m{ a }^{ 3 }\epsilon }$ hope you can calculate the rest

The electric field due to a charged ring of radius $R$ having charge $q$ at a point on its axis is given by

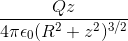
If $z << R$ then $(R^2 + z^2)^{3/2}$ $=$ $R^3$ as we neglect the $z^2$ term.

Multiplying the electric field by charge $-Q$ (charge of particle) we get the force $F$ acting on particle. ( $F = -EQ$ )

The equation is then of the form $F = -kz$ (minus sign appears because charge is negative and force is thus restoring.)

Or alternatively dividing by m we have $a$ $=$ $-ω^2z$ clearly indicating SHM .

Thus we have the time period as $T = 2π / ω$ giving way to ,

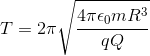
after slight re-arrangement,

$b = 3$

$c = 3$

$d = 0.5$

$e = 16$

$b+c+d+e = 22.5$

---

Derivation of the equation:

Consider an element $dx$ having charge $dq$ of the ring.as we can see all such $dq$ 's will be at equal distance $r$ from point $z$ .As we can see if we consider another $dq$ element symmetrically opposite to the first one,the $x$ components of the electric fields get cancelled out,only $y$ components remains and the expression for it is shown below.

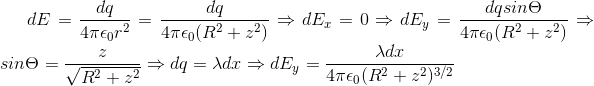
Thus integrating ,

---

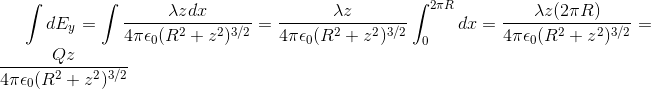
Note: Unlike previous answer here i have measured the angle with respect to vertical that is ring.Hence my sine is his cosine.