SHM in liquid
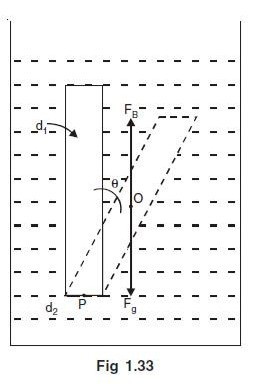 A thin rod of length
and area of cross section
is pivoted at its lowest point P inside a stationary , homogeneous , non viscous liquid as shown in the figure.
A thin rod of length
and area of cross section
is pivoted at its lowest point P inside a stationary , homogeneous , non viscous liquid as shown in the figure.
The rod is free to rotate in a vertical plane about a horizontal axis passing through . The density of the material of the rod is smaller than the density of liquid . The rod is displaced by a small angle from its equilibrium position and then released.
If the body performs Simple harmonic motion, calculate t's angular fequency
Details and Assumptions
Also try this.
The answer is 8.66.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
.
The different forces on the rod are:
Weight of the rod acting downwards = m g = S L D 1 g
Buoyant force acting upwards = S L D 2 g
Net thrust acting on the rod upwards; F = S L ( D 1 − D 2 ) g
Restoring torque τ = F 2 L s i n θ
If θ is in clockwise direction then τ will be in anticlockwise direction
τ = - F 2 L s i n θ
Also τ = I α
Where I = 3 M L 2
Find α using above equation and then find angular frequency ω using differential equation of S . H . M
U will get ω = 2 L 3 g D 1 D 2 − D 1