Shortest cut line for tetrahedron surface
To obtain a plane scan of the tetrahedron, it is necessary to make a cut of the surface. Find the minimum length of the cut line of the tetrahedron surface to obtain a flat surface scan. Find minimum length of cut for tetrahedron edge equal 1.
If the answer can be expressed as W , where W are positive integers and W is square-free, give the value of W .
For picture
L
c
u
t
=
1
+
3
- not minimal length.
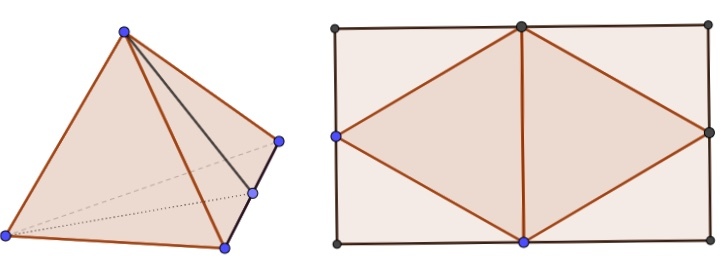
Solution use approach
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you post a solution to the cube problem?
https://brilliant.org/problems/shortest-cut-line-for-cube-surface/
Since vertices are the only 'non flat' points, the cut has to connect these points to get a plane scan. That means that the least number of faces the cut is located in is two. Thus, we need to connect 4 vertices of adjacent equilateral triangles as short as possible. It is known fact that the shortest way to connect 4 points is graph with two additional points whose angles between them equal 120°:
Due to symmetry point M is the middle of section BC and point E' is symmetrical to point E.
For a given equilateral triangle ABC and point M we need to find point E. To do this let's draw an equal triangle ABC' and inscribe it in circumference. Let's prove that the section C'M intersect with the circumference at sought point E:
Angles ∠BAE and ∠BC'E both inscribed and lean on the same arc, which means ∠BAE = ∠BC'E = α. Then ∠CAE = 60° - α, ∠CME = 180° - ∠BME = 180° - ∠BMC' = ∠BC'M + ∠C'BM = ∠BC'E + ∠C'BC = ∠BAE + 120° = α + 120°. We got that ∠CAE + ∠CME = 180° which means that quadrangle ACME is inscribed. From that we can conclude that ∠AEM = 180° - ∠ACM = 120°. Angle ∠AEB is inscribed in circumference and is opposite to angle ∠AC'B, which means ∠AEB = 180° - ∠AC'B = 180° - 60° = 120°. Thate means that ∠AEB = ∠AEM = ∠BEM = 120°. Thus we found point E:
All that is left is to find the length of the cut:
(MC')^2 = (MB)^2 + (BC')^2 - 2cos∠C'BM MB BC' = ( 4 1 ) + 1 - 2cos120° 2 1 = ( 4 1 ) + 1 + 2 1 = 4 7
MC' = 2 s q r t ( 7 )
∠BAE = ∠BC'E = α and ∠AEB = ∠C'BM = 120° and we have two homothetic triangles ABE and BC'M. That implies:
A B A E = M C ′ B C ′ and A B B E = M C ′ B M
AE = s q r t ( 7 ) / 4 1 = 7 4 s q r t ( 7 ) , BE = s q r t ( 7 ) / 4 0 . 5 = 7 2 s q r t ( 7 )
ME = MC' - EC' = MC' - AC' = 2 s q r t ( 7 ) - 1 = 2 s q r t ( 7 ) − 2
AE, BE and ME form just a half of the cut:
Length of cut = 2(AE + BE + ME) = 2( 7 6 s q r t ( 7 ) + 2 s q r t ( 7 ) − 2 ) = 7 1 2 s q r t ( 7 ) + sqrt(7) - 2 = 7 1 9 s q r t ( 7 ) − 1 4
(Sorry, I can't use LaTeX)
It's a surprisingly neat and beautiful numerical result. Unexpected.
F C 2 = F B 2 + B C 2 − 2 B C ⋅ F B ⋅ c o s 1 2 0 ∘ = 7
Second variant - calculate sides a , b , c of triangles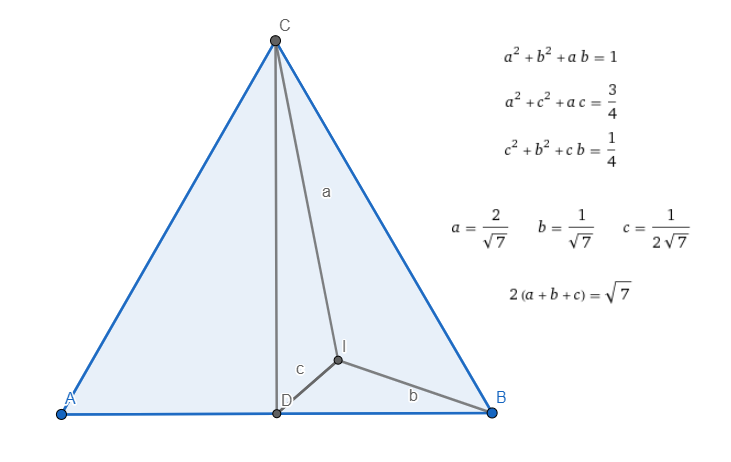 wolframalpha calculate
wolframalpha calculate
The answer is 7 .