Shortest distance on the surface of a dodecahedron
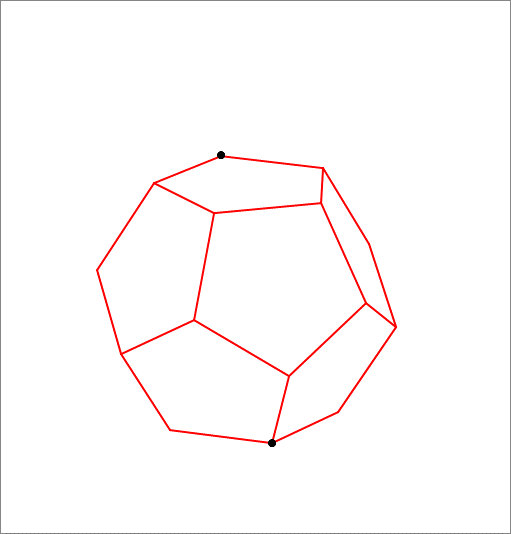
Given a regular dodecahedron of unit edge length, find the shortest distance on the surface of the dodecahedron between two opposite vertices. If the distance is then find .
Hint: Unfold (unwrap) the faces of the dodecahedron, then apply the Law of Cosines.
The answer is 4040.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The following animation illustrates unfolding of the faces of the dodecahedron.
The last frame from above is repeated below with the distance d as one side of the triangle, the other two sides are of lengths 2 h and 1 where h is the altitude of the pentagonal face, and the angle between these two sides is 5 4 ∘ + 1 0 8 ∘ .
The altitude of a unit edge length pentagon is h = sin ( 1 0 8 ∘ ) + sin ( 1 0 8 ∘ − 7 2 ∘ ) = 1 . 5 3 8 8 4 1 7 6 9
Applying the Law of Cosines, the required distance is
d = ( 2 h ) 2 + 1 − 4 h cos ( 5 4 ∘ + 1 0 8 ∘ ) = 4 . 0 4 0 5 7 3 9 5 9 , which makes the answer 4 0 4 0 .