Shortest Distance Problem
Calculus
Level
3
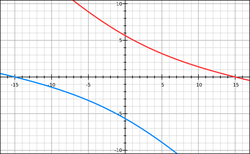 Find the shortest distance from the origin to the hyperbola
.
Find the shortest distance from the origin to the hyperbola
.
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us take an arbitrary line through the origin y = m x that intersects the above hyperbola in the points;
x 2 + 8 x ( m x ) + 7 ( m x ) 2 = 2 2 5 ⇒ ( 1 + 8 m + 7 m 2 ) x 2 = 2 2 5 ⇒ x = ± 1 + 8 m + 7 m 2 1 5 and y = ± 1 + 8 m + 7 m 2 1 5 m .
Let L ( m ) = x 2 + y 2 = ( 1 + 8 m + 7 m 2 1 5 ) 2 + ( 1 + 8 m + 7 m 2 1 5 m ) 2 = 1 5 ⋅ 1 + 8 m + 7 m 2 1 + m 2 ;
be the distance from the origin to either of these points and taking d m d L = 0 gives:
d m d L = 2 1 5 ⋅ 1 + m 2 1 + 8 m + 7 m 2 ⋅ ( 1 + 8 m + 7 m 2 ) 2 ( 2 m ) ( 1 + 8 m + 7 m 2 ) − ( 1 + m 2 ) ( 8 + 1 4 m ) = 0 ⇒ m = 2 , − 2 1 .
Upon observation, the hyperbola has negative slopes in both of its branches. The shortest distance from the origin to the hyperbola will occur along a line that is normal to the hyperbola (i.e. the product of m and the slope of the hyperbola's tangent must equal -1). This in turn forces the critical value of m to be positive (discounting m = − 2 1 ).
Hence, the shortest distance from the origin to the hyperbola occurs along the line y = 2 x and computes to L ( 2 ) = 5 .