Shortest distance
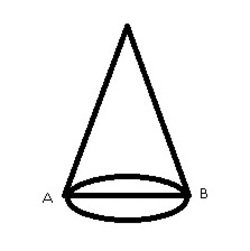 The cone shown above has a height of 1m and the base radius is 2m. An ant sits at point A. He has to move over the curved surface to point B which is diametrically opposite. What is the shortest distance from A to B in metres correct to 3 decimals.
The cone shown above has a height of 1m and the base radius is 2m. An ant sits at point A. He has to move over the curved surface to point B which is diametrically opposite. What is the shortest distance from A to B in metres correct to 3 decimals.
The answer is 4.411.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Here is an illustration of the laid-out surface area of the cone.
We want to find X . We can get it by using the fact that dividing θ in half will give us two right triangles (as seen in the picture), from which we can use trigonometry to get it.
S = h 2 + r 2 = 5
θ = S π r = 5 2 π
X = 2 × ( S s i n ( 2 θ ) ) = 2 5 s i n ( 5 π )
≈ 4 . 4 1 1