Shortest Path #2
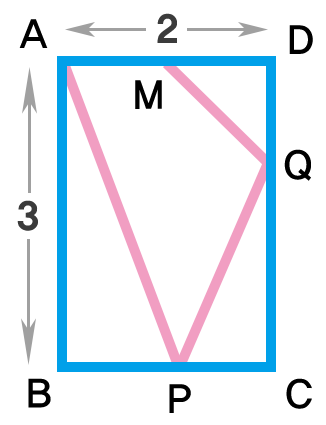
There is a rectangle A B C D with side lengths 2 and 3 as shown on the right.
Point P is on B C and point Q is on C D .
M is the midpoint of A D .
Let m be the length of the shortest path from A to M , while visiting P and Q sequentially.
Find the value of m 2 .
This problem is a part of <Shortest Path> series .
The answer is 45.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
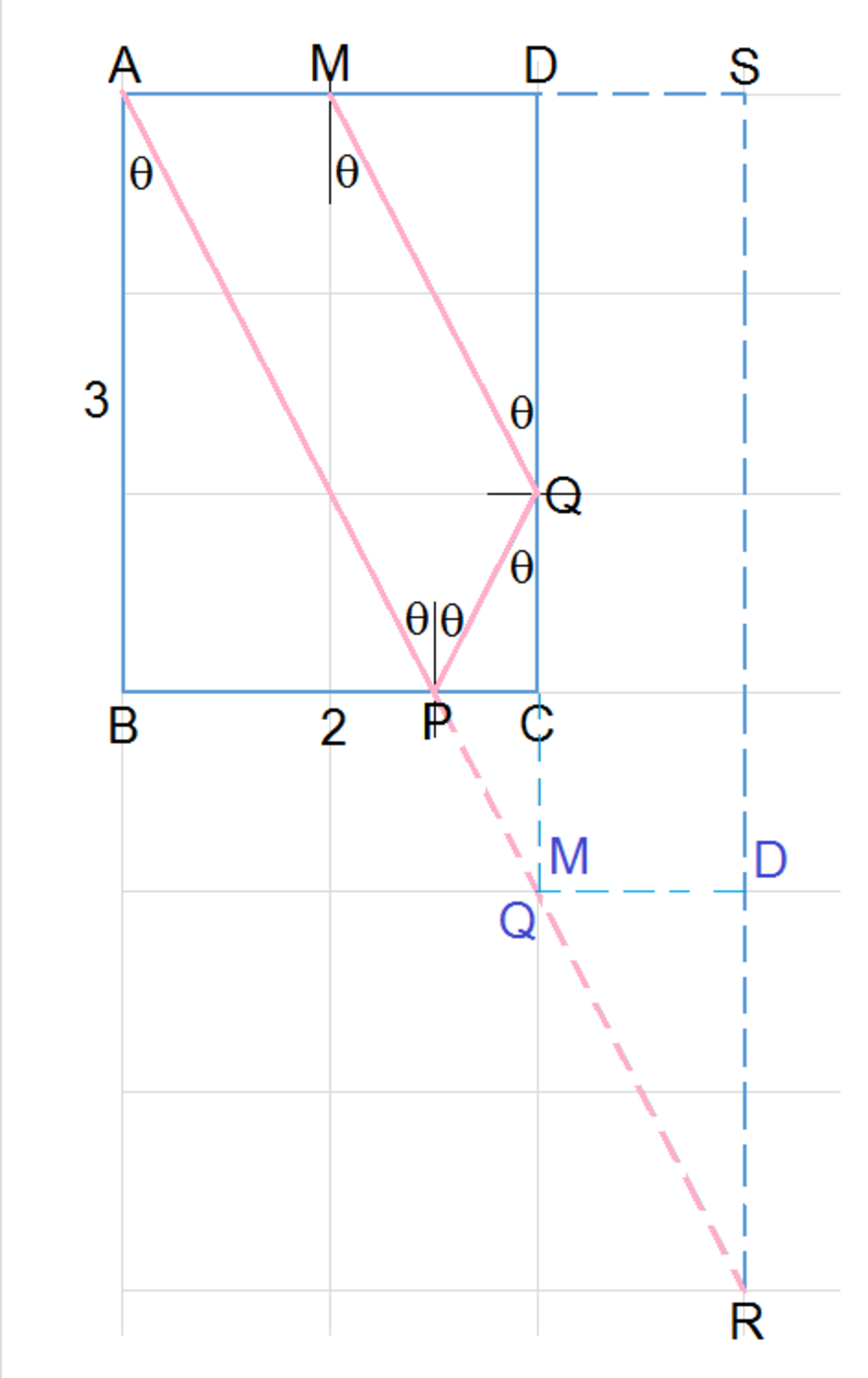
The shortest distance traveled from A to M is that traveled by light. Therefore, the sides B C and C D acts like mirrors where line A P incidents at an angle of θ and reflects at the same angle of θ . If we fold the reflected beams at the mirrors, we find that the image P R is colinear with incident beam A P making A R a straight line as expected of how light should travel.
We note that the light beam travels vertically a distance of R S = A B + C D = 3 + 3 = 6 and horizontally S M = B C + D M = 2 + 1 = 3 . By Pythagorean theorem , A R 2 = R S 2 + S M 2 , ⟹ m 2 = 6 2 + 3 2 = 4 5 .
Image A on BC is A', BA'=AB and ABA' is a st. line.
Image M on DC is M', DM'=MD and MDM' is a st. line.
Shortest distance=m=A'M'=
A
A
′
2
+
A
M
′
2
.
∴
m
2
=
(
3
+
3
)
2
+
(
1
+
1
+
1
)
2
=
4
5
.
I missed since pressed discuss button!
We are trying to minimize A P + P Q + Q M .
Rotate the rectangle about point C for 1 8 0 ∘ to get rectangle A ′ B ′ C D ′ .
Note that P Q = P Q ′ and Q M = Q ′ M ′ .
Also, it is clear that A P + P Q ′ + Q ′ M ′ ≥ A M ′ .
Therefore A P + P Q + Q M = A P + P Q ′ + Q ′ M ′ ≥ A M ′ = 3 5 .
∴ m 2 = ( 3 5 ) 2 = 4 5 .