Shortest Path #3
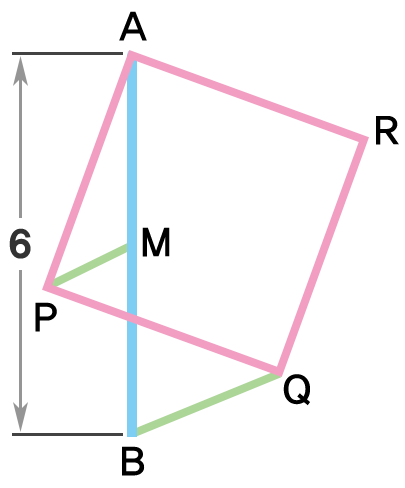
As shown on the right, there is a line segment
Pick a point and draw a square that has as one of its sides, such that and intersect.
Let be the midpoint of
Then is the length of the shortest path from to while visiting sequentially.
Given that are integers and is square-free, find the value of
This problem is a part of <Shortest Path> series . The series is gonna keep getting harder, so be prepared!
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We are trying to minimize A P + P M + B Q + B M .
Draw a square A M X Y like the image on the left.
We can prove that △ A M P ≡ △ A Y R , and thus P M = R Y .
Also note that R Y + R Q + B Q ≥ B Y .
Therefore
A P + P M + B Q + B M = R Q + R Y + B Q + 3 ≥ B Y + 3 = A B 2 + A Y 2 + 3 = 3 + 3 5 .
with equality achieved when Q and R lies on B Y .
∴ a + b + c = 3 + 3 + 5 = 1 1 .