Shortest Path off the Sides of an Equilateral Triangle
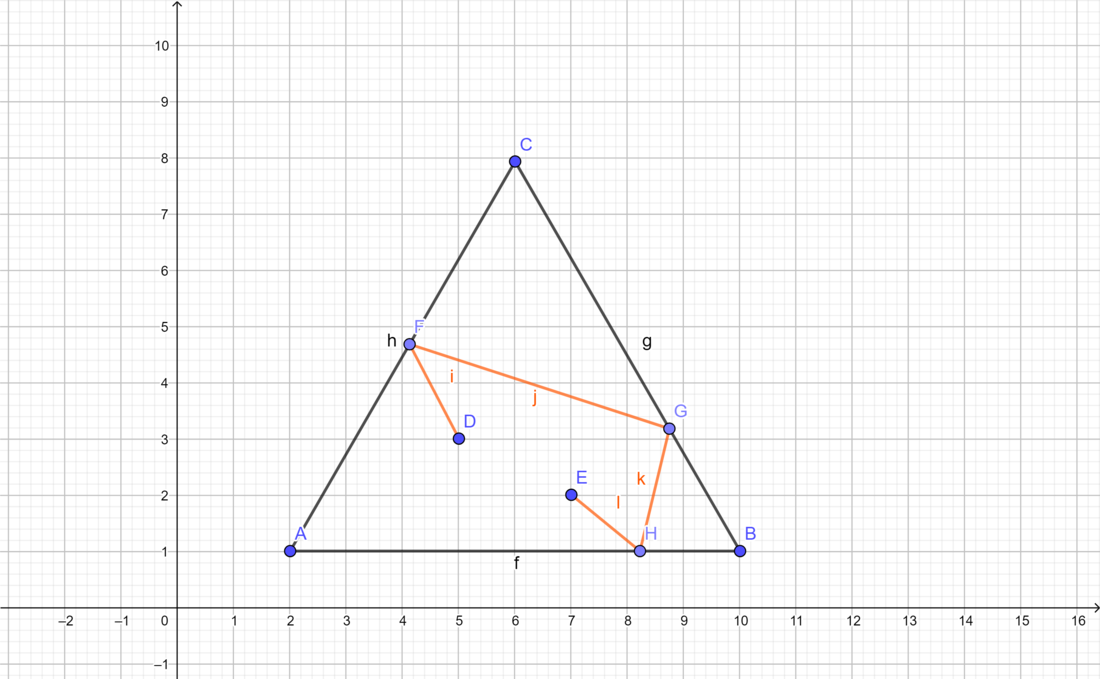
△ A B C is an equilateral triangle of side length 8 with A = ( 2 , 1 ) , B = ( 1 0 , 1 ) , C = ( 6 , 1 + 4 3 ) . Points D ( 5 , 3 ) , and E ( 7 , 2 ) are inside the triangle. You want to travel from point D to point E off the sides of the triangle in the order A C , B C , A B , as illustrated in the above figure. Find the shortest possible path from D to E under these conditions. The shortest path length can be expressed as d = a − b c for positive integers a , b , c with c square-free. As your answer, enter a + b + c .
The answer is 138.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
That's how I did it!
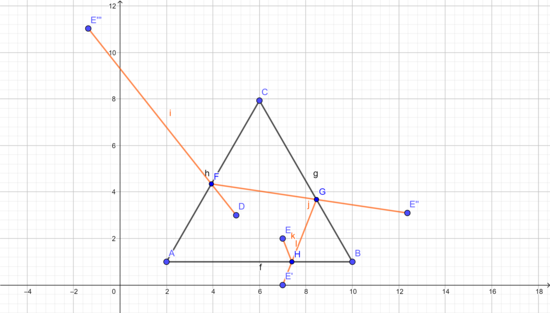
The above figure shows how to find the shortest path by reflecting the end point (point E ) about the sides in reverse order, so first about side A B and this generates point E ′ . Then we reflect point E ′ about side B C generating point E " , and finally we reflect E " about A C generating point E ′ ′ ′ . The distance D E ′ ′ ′ is the shortest distance. The coordinates of E ′ ′ ′ = ( − 2 1 − 2 3 , 2 1 1 3 + 2 3 ) , and this makes the distance D E ′ ′ ′ = 1 2 4 − 1 1 3 . Hence the answer is 1 2 4 + 1 1 + 3 = 1 3 8
The shortest path between two points D and E is one taken by a beam of light. Treat sides of the equilateral triangle as mirrors where the beam of light reflects off. We can find the image light path by reflecting the triangle about the mirrors.
Starting from D ( 5 . 3 ) , we find the final image of E is at E ′ ( − 2 1 + 3 , 2 3 + 1 1 3 ) . Therefore the shortest length of the path is ( 5 + 2 1 + 3 ) 2 + ( 3 − 2 3 + 1 1 3 ) 2 = 1 2 4 − 1 1 3 , and a + b + c = 1 2 4 + 1 1 + 3 = 1 3 8 .