Shortest separation
What is the shortest distance between the circle x 2 + ( y + 6 ) 2 = 1 and the parabola y 2 = 8 x ?
The answer is 1.828.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
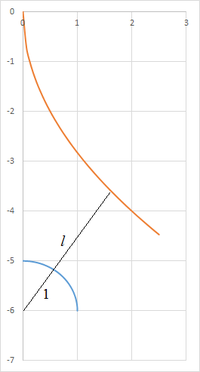
Note that x 2 + ( y + 6 ) 2 = 1 is a circle centered at ( 0 , − 6 ) with radius 1 . The shortest distance between the circle and parabola is from the negative half of the parabola that is from a point ( x , − 8 x ) . Let the distance between the center of the circle and the parabola be l = ( x − 0 ) 2 + ( − 8 x + 6 ) 2 . Then the distance between the circle and parabola is l − 1 . And we have:
l − 1 = x 2 + ( 6 − 8 x ) 2 − 1 ≥ 2 x + 6 − 8 x − 1 = 2 2 + 6 − 1 6 − 1 = 2 2 − 1 = 1 . 8 2 8 By Titu’s lemma Equality occurs when x = 6 − 8 x ⟹ x = 2
Reference: Titu's lemma
We want the point P on the parabola and the point C on the circle so that C P is perpendicular to the tangent to the parabola at P , and perpendicular to the tangent to the circle at C . But then C P is parallel to the radius of the circle at C , and hence passes through the centre ( 0 , − 6 ) of the circle. Thus, if P has coordinates ( x , y ) , then C P has gradient x y + 6 . The gradient of the tangent at P is y 4 , and so we require x y + 6 = − 4 y , so that x = − 4 − y 2 4 . But then y 2 y 3 + 3 2 y + 1 9 2 = 8 x = − 3 2 − y 1 9 2 = 0 and the only real solution of this equation is y = − 4 . Thus P has coodinates ( 2 , − 4 ) , so the distance from P to the centre of the circle is 2 2 , and hence the minimum distance C P = 2 2 − 1 .