Shortest Sierpinski Walk
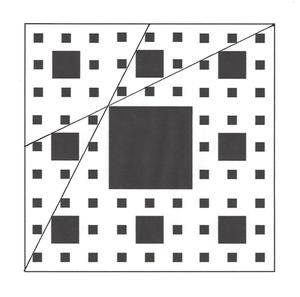
This is a Sierpinski carpet, bounded by a unit square.

The largest white square has 3 1 the side length of the unit square, the next largest white squares have 3 1 the side length of the largest, etc. The construction of this fractal starts with dividing a black unit square into 9 equal squares, of which the center is made white and all the rest are left black; then each of the remaining 8 squares is likewise divided into 9 equal squares, of which the center is made white and all the rest are left black, etc., which continues infinitely many times.
What is the length of the shortest path between 2 opposite vertices of the unit square, which does not travel across any of the white squares? The distance can be expressed as c a b , where a , b , c are positive integers, a and c are coprime, and b is square-free.
What is the sum a + b + c ?
Note: Only the interior of the white squares are removed, i.e. the boundaries are left available for any pathway. For example, pathways may include vertices of "white squares."
Note of interest: This Sierpinski carpet has an area of 0 , which may not be relevant to this problem.
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Calvin, this is a proof with a lot less hand-waving than the one I posted. First, I liked the idea of using decimal representation in base 3 . Secondly, I liked the crux Proof of existence , which nails it. I was about to post a "proof" arguing that if the line does pass through a black square not through its vertex, then that square would have to be created at some n th iteration, which means it would recursively happen infinitely many times, either n + + or n − − (i.e., in the latter case, creation of larger squares not smaller), but that would only be more hand-waving. It's also important to establish that points exists at all for a continuous path to travel, as we have to be mindful that the area of a Sierpinski Carpet is 0 as the limit.
Your proof gives me something to think about.
Log in to reply
It took me a while to figure out the best way to prove that claim, and I like this solution.
@Jason Dyer also wanted to take the approach of "self-similarity, sometimes with rotate by 1 8 0 ∘ ", and argue that each time no dots are removed.
If you break the figure into a 3x3 grid you get self-similar chunks, and you can use that to show no fractal iteration will break the solution. This would result in a more elementary proof. You're welcome to steal this for your own solution.
Log in to reply
Jason, proving that the straight line in question doesn't cross white squares is only half of the story. What also has to be proven is that there are sufficient points not inside white [black] squares that will permit a continuous path over the entire length. Remember, the area of a Sierpinski Carpet is 0 as the limit.
This graphic is a negative of the other one shown, i.e., white → black, black → white
Draw a line from one vertex of the unit square to the midpoint of the other side, as shown in graphic. This line passes through the vertex of the largest white [black] square. Hence, if all the other sub-squares are constructed in a like manner, this line also passes through the vertex of the largest white [black] square of each, no matter how small. Homothety, anyone? The distance from the vertex of the unit square to the vertex of the largest white [black] square then works out to
3 1 5
so that for the total path, a + b + c = 2 + 5 + 3 = 1 0
Should we clarify that it's the interior of the square that has been removed, so (say) the point ( 3 1 , 3 2 ) still exists for the path to be on?
Log in to reply
Yeah, I should clarify that. Real analysis has always been one of my weak subjects in school.
This graphic is a negative of the other one shown, i.e., white → black, black → white. The white space indicates the possible routes to walk on.
Classification of Sierpinski carpet: The point ( x , y ) exists in the Sierpinski carpet if and only if in the base 3 representation x = 0 . x 1 x 2 x 3 … , y = 0 . y 1 y 2 y 3 … ,
1. There is no value of n such that ( x n , y n ) = ( 1 , 1 ) , OR
2. If there is a value of n such that ( x n , y n ) = ( 1 , 1 ) , then either for x N = 0 for all N > n or y N = 0 for all N > n .
Note: For clarity, we take the "simplified form", where we disallow the eventual repeating decimal 2 2 2 … .
Proof of classification: This follows because at the n th iteration, the squares that are removed are those with ( x n , y n ) = ( 1 , 1 ) . The second condition is to add back the left and bottom sides of the square since we only removed the interior.
Claim: The route that we're looking for, is the line connecting the points from ( 0 , 0 ) to ( 3 1 , 3 2 ) and then to ( 1 , 1 ) . (The symmetric route to the point ( 3 2 , 3 1 ) also works.
Proof of minimality: When we remove the first central square, we already see that this path is the shortest possible. More formally, let's separate the square into 2 parts with the line y = 1 − x . Then, the shortest distance out of the lower left half would be from ( 0 , 0 ) to ( 3 1 , 3 2 ) OR from ( 0 , 0 ) to ( 3 2 , 3 1 ) . Similarly, for the upper right half, the shortest distance is from ( 1 , 1 ) to ( 3 1 , 3 2 ) OR ( 1 , 1 ) to ( 3 2 , 3 1 ) . This establishes that the path we chose, is the shortest possible in the first iteration.
We cannot hope to do better, since in subsequent iterations, more area is removed.
Proof of existence: The bigger question is why this path continues to exist throughout all iterations of removing central squares. Let's consider the first half of the path (under the line y = 1 − x ), and the second half is dealt in a similar manner.
We will prove by contradiction that the points lying on y = 2 x , 0 ≤ x ≤ 3 1 lie on the Sierpinski carpet.
Suppose not. Then, there is a point ( x , y ) with y = 2 x and x n = y n = 1 .
Observe that the fractional part of 3 n − 1 × 2 x looks like 0 . 2 ( 2 x n + 1 ) ( 2 x n + 2 ) … ≥ 3 2
and the fractional part of 3 n − 1 × y looks like 0 . 1 y n + 1 y n + 2 … < 3 2 .
Hence, the fractional part of 3 n − 1 ( 2 x − y ) is non-zero, and so this term cannot be 0.
This contradicts y = 2 x .