Shortest way out

Geometry Level 2

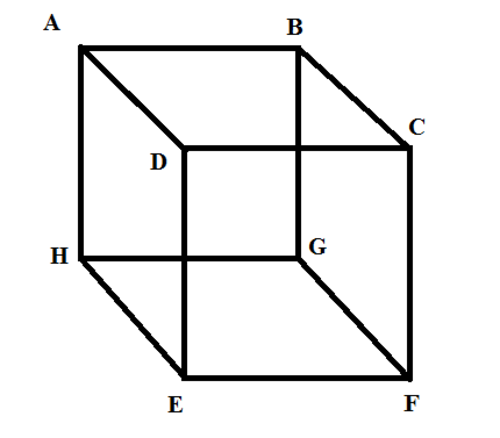Above is a cube $ABCDEFGH$ . $ABCD$ is the ceiling, $EFGH$ is the floor, and the rest are the walls. Additionally, $AB = 2$ . A lizard is on point $F$ and is wanting to go to point $A$ . If the lizard can only travel via walls, what is the measure of the shortest distance the lizard can take in order to reach its destination?

The answer can be expressed in the form of $A + B\sqrt{C}$ such that $A$ , $B$ and $C$ are prime numbers or $0$ . Find $A + \frac{C}{B}$ .

The answer is 2.5.

2 solutions

Eric Escober
Apr 9, 2015

Shortest path is through two walls. You can see it as $unfolding$ the walls into a two-dimensional figure (as seen below). Then do the rest. (Please be considerate of my MSPaint solution. hehe)

Emmanuel John Baliwag
Jan 10, 2015

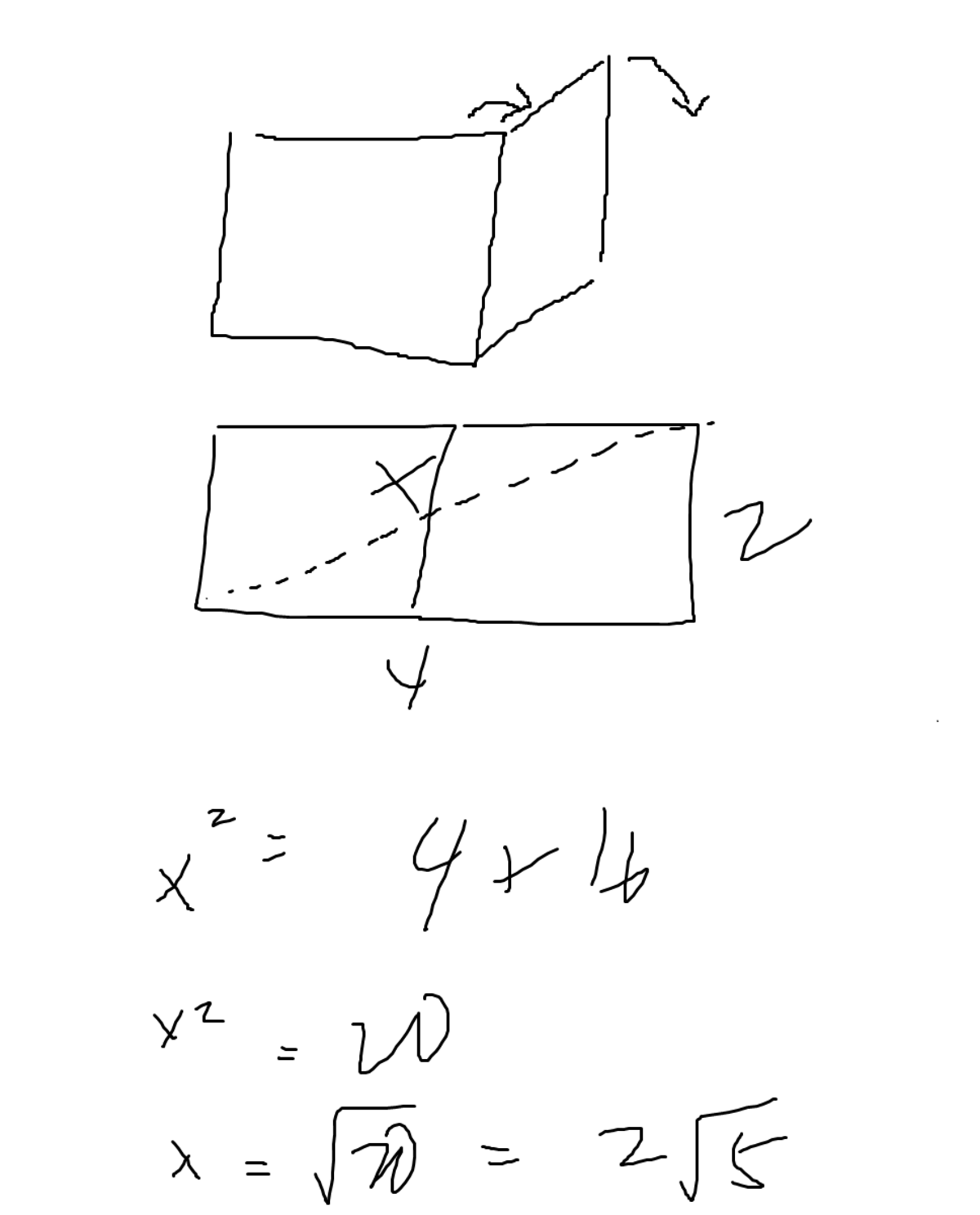
For a cube, to access the opposite non-coplanar corners, the shortest distance is the diagonal. Since the lizard is restricted to only the walls, it can't use it. Let $M$ be the midpoint of $D$ and $E$ . Since $DE = 2$ , $DM = ME = 1$ . Connecting $F$ , $M$ , and $A$ we can get the possible shortest distance. $FM = MA =$ $\sqrt{1^2 + 2^2} = \sqrt{5}$ The shortest distance is $FM + MA$ which is equal to $2\sqrt{5}$ . The answer should be $A + \frac{C}{B}$ . We have $A = 0$ , $B = 2$ , $C = 5$ . And $\frac{C}{B}$ $=$ $\frac{5}{2}$ $= \boxed{2.5}$

Shortest way out

The answer is 2.5.

2 solutions

0 pending reports