Should I plot them? 2

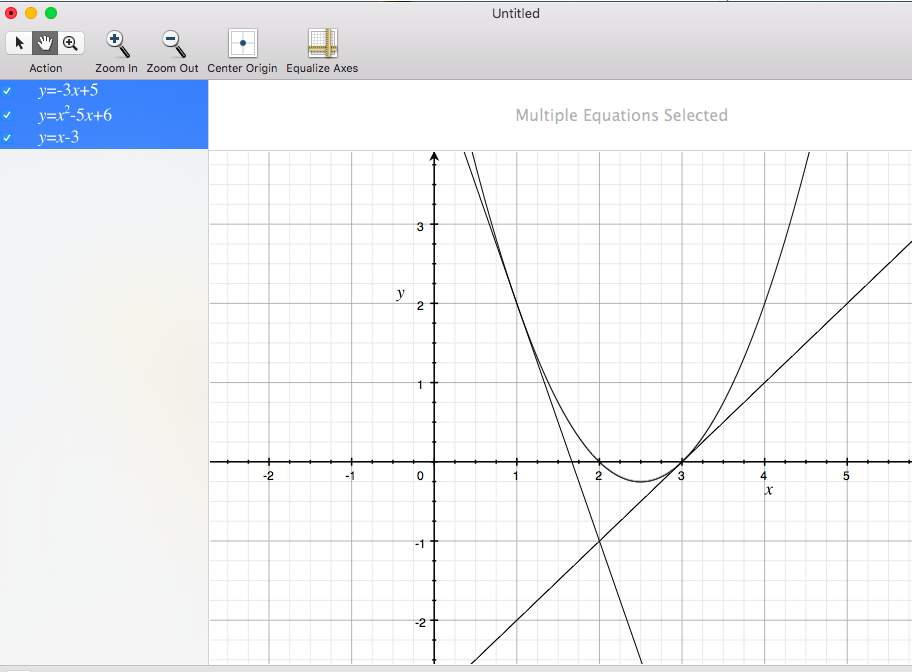
Both the questions in series 'Should I plot them?' have been taken from Calculus Made Easy by Silvanus P. Thompson. Both of them are interesting questions indeed.

First of all we consider the points $A(x_1,y_1)$ and $B(x_2,y_2)$ as tangency points on the curve $y=x^2-5x+6$ . It is self evident at these points the slope of tangents passing through $(-2,1)$ must be equal to that of curve.

Let the equation of tangent line be $y=mx+c$ (we will consider only one line here). Clearly ' $m$ ' is the slope of line.

Slope of the curve $\frac{dy}{dx}= 2x-5$ ,

So,

$m=2x-5$

Also,

The the equation must satisfy $(2,-1)$ , so $-1=2m+c$ or $c=-2m-1$

Now solving for points $A$ and $B$ by equating the equation of tangent line to that of the curve.

$x^2-5x+6=(2x-5)x-(2x-5)-1$

$x^2-4x+3=0$

$x=x_1=3$ or $x=x_2=1$

So,

$A(3,0)$ and $B(1,2)$

(not a solution.) @Brian Charlesworth

The given solution is correct, I think.