Should I use trig?
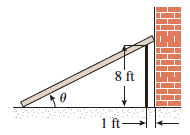
A plank is used to reach over a fence 8 ft high to support a wall that is 1 ft behind the fence. What is the length of the shortest plank that can be used? Round your answer to the nearest tenths.
Problem credit: Calculus by Anton, 10th Ed.
The answer is 11.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let L be the length of the plank and x the distance from the base of the plank to the base of the fence. Since the triangles formed by: (i) the plank, ground and fence and (ii) the plank, ground and wall, are similar, we see that
x + 1 L = x x 2 + 8 2 ⟹ L = ( 1 + x 1 ) x 2 + 6 4 .
Then by the product rule we have that
d x d L = ( − x 2 1 ) x 2 + 6 4 + ( 1 + x 1 ) ∗ x 2 + 6 4 x =
x 2 + 6 4 1 ( − x 2 ( x 2 + 6 4 ) + ( 1 + x ) ) = x 2 + 6 4 1 ∗ ( − x 2 6 4 + x ) .
Now d x d L = 0 when x 2 6 4 = x ⟹ 6 4 = x 3 ⟹ x = 4 .
As we could have the plank stretch out to infinity, it is clear that the critical point at x = 4 will yield a minimum, and this minimum is
L ( 4 ) = ( 1 + 4 1 ) 1 6 + 6 4 = 4 5 ∗ 5 ∗ 1 6 = 5 5 = 1 1 . 2 ft. to one decimal place.