Should you simplify?

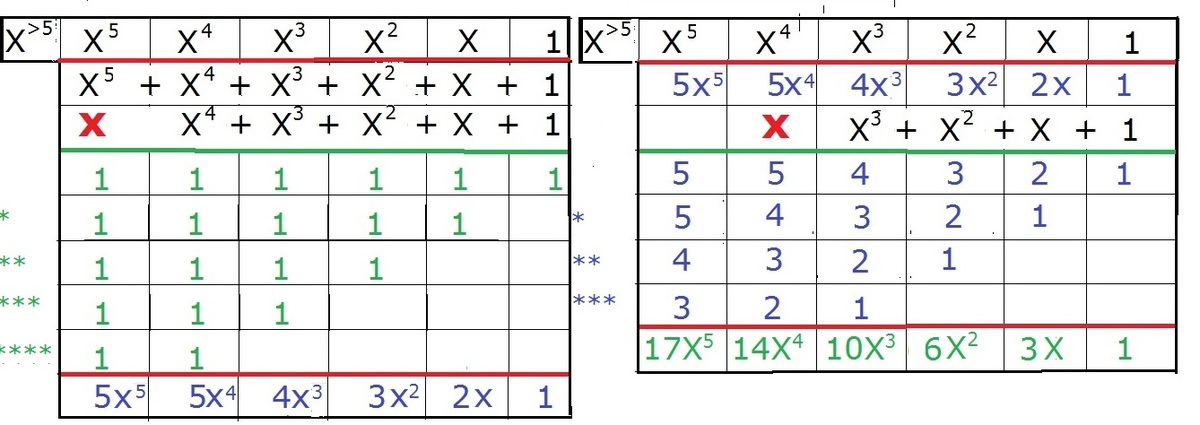
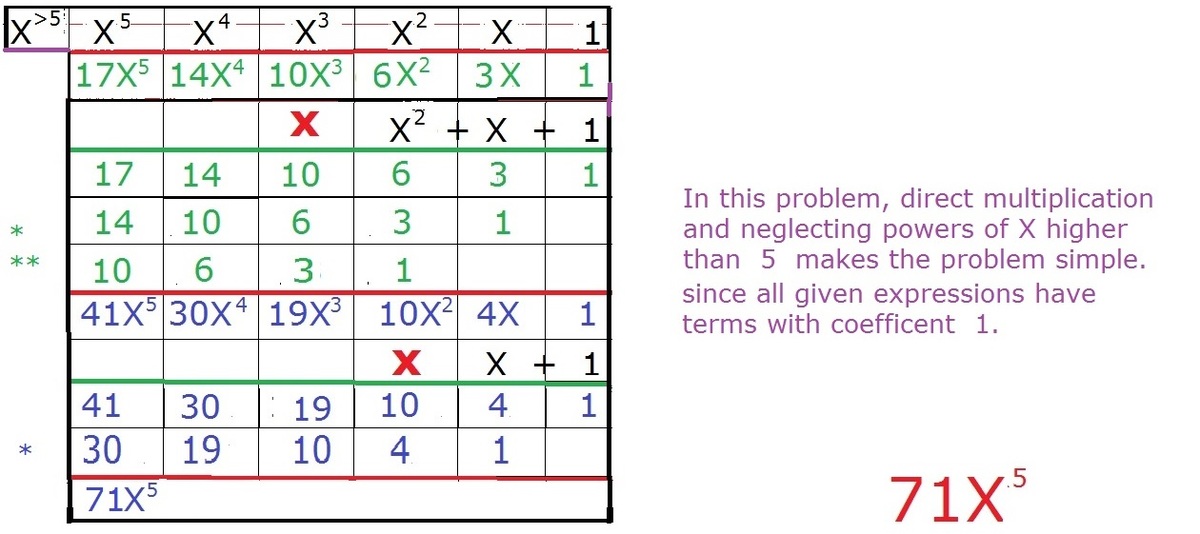
This is simply $(1-x^2)(1-x^3)(1-x^4)(1-x^5)(1-x^6)\sum_{k = 0}^{\infty}{{k+4 \choose 4}x^{k}}$ so the $x^5$ coefficient is ${9 \choose 4} - {7 \choose 4} - {6 \choose 4} - {5 \choose 4} = \boxed{71}$ .

Another way: The $x^5$ coefficient is exactly the number of ways to choose 5 balls among $1$ red, $2$ green, $3$ yellow, $4$ black, and $5$ white balls where balls of the same color are indistinguishable. Let $a_{color}$ denote the number of balls that are chosen for the color. We see that $a_{r} + a_{g} + a_{y} + a_{b} + a_{w} = 5$ We will use PIE and Stars and Bars.

By stars and bars this is ${9 \choose 4}$ ways.

If $a_r \geq 2$ , then we have ${7 \choose 4}$ ways.

If $a_g \geq 3$ , then we have ${6 \choose 4}$ ways.

If $a_y \geq 4$ , then we have ${5 \choose 4}$ ways.

If $a_b \geq 5$ , then we have ${4 \choose 4}$ ways.

If $a_r \geq 2$ and $a_g \geq 3$ , we have ${4 \choose 4}$ ways.

The rest are zero. Therefore by PIE, the total valid ways are ${9 \choose 4} - {7 \choose 4} - {6 \choose 4} - {5 \choose 4} - {4 \choose 4} + {4 \choose 4}$ which is exactly what we got above.