Shoutout to MathForLove!

Let $ABCD$ be a quadrilateral, and $EFGH$ be the new quadrilateral that is formed by joining the midpoints of adjacent sides.

Then each side of $EFGH$ is a midsegment of a triangle whose base is one of the diagonals of $ABCD$ and whose sides are two of the sides of $ABCD$ . By the triangle midsegment theorem, $EF || AC$ and $GH || AC$ , so $EF || GH$ . Similarly, $FG || BD$ and $EH || BD$ , so $FG || EH$ . Therefore, $EFGH$ must be a parallelogram.

Now let $BK$ be the altitude of $\triangle ABC$ and $J$ the intersection of $BK$ and $EF$ (for concave quadrilaterals, let $A$ be the concave angle, and extend $EF$ for the intersection point $J$ ). Similarly, let $DL$ be the altitude of $\triangle ACD$ and $M$ the intersection of $DL$ and $GH$ . Let $p = EF$ , $q = JK$ , and $r = LM$ .

Once again by the triangle midsegment theorem, $EF = \frac{1}{2}AC$ , and since $p = EF$ , $AC = 2p$ . Since $\triangle BEF \sim \triangle BAC$ and corresponding sides $EF$ and $AC$ have a $\frac{1}{2}$ ratio, the heights $BJ$ and $BK$ also have a $\frac{1}{2}$ ratio, and since $q = JK$ , $BK = 2q$ . Similarly, since $r = LM$ , $DL = 2r$ .

The area $A_{ABCD}$ of quadrilateral $ABCD$ is equivalent to the combined areas of $\triangle ABC$ and $\triangle ADC$ , which are $\frac{1}{2} \cdot 2p \cdot 2q = 2pq$ and $\frac{1}{2} \cdot 2p \cdot 2r = 2pr$ respectively, so $A_{ABCD} = 2pq + 2pr = 2(pq + pr)$ . The area $A_{EFGH}$ of parallelogram $EFGH$ is $A_{EFGH} = p(q + r) = pq + pr$ . Therefore, $A_{EFGH} = \frac{1}{2}A_{ABCD}$ .

The above argument can be made for any quadrilateral $ABCD$ , whether it be a square, rectangle, concave, or convex. Therefore, if the midpoints of adjacent sides of any quadrilateral are joined, a parallelogram is always formed that is always half of the area of the original quadrilateral.

It could be any quadrilateral.

Without loss of generality:

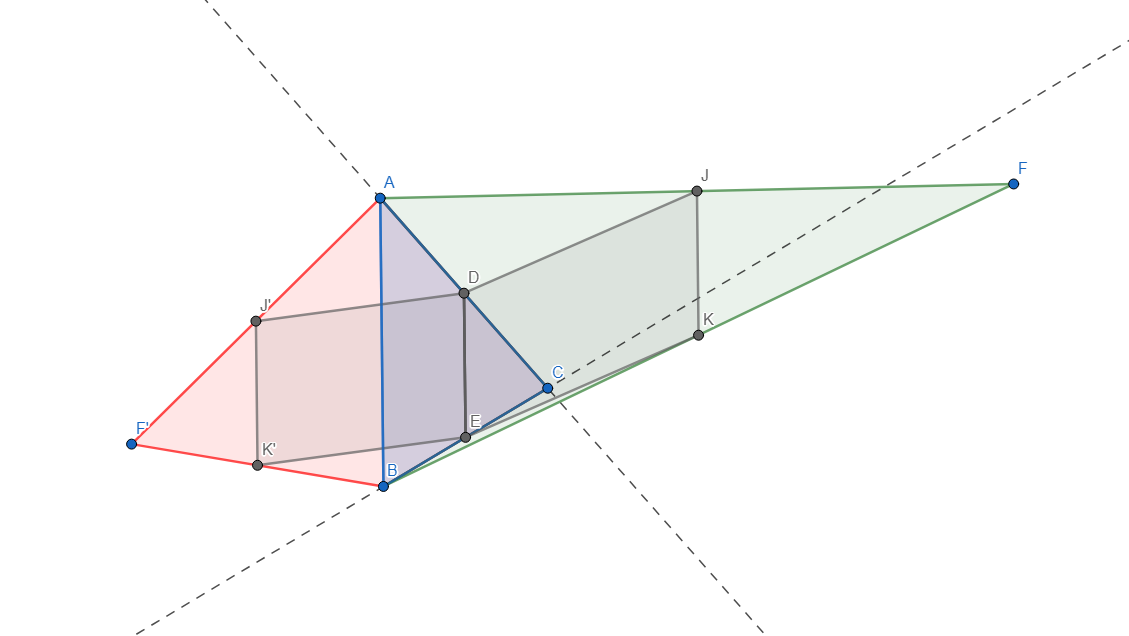
• Start out by drawing a random triangle $ABC$ .

• Identify midpoints of sides $AC$ and $BC$ and denote them with $D$ and $E$ , respectively. By similarity of triangles, it follows that $AB || DE$ and $AB = 2DE$ .

• Take any point in the space bounded by dashed lines and denote it with $F$ . Denote the midpoints of segments $AF$ and $BF$ with $J$ and $K$ , respectively. Again, by similarity of triangles, it follows that $AB || JK$ and $AB = 2JK$ .

• We deduce that $DE || JK$ and $DE = JK$ , quod erat demonstrandum.

Proposed correct answer (selecting all three options) is misleading. In my opinion, the correct answer should be selecting only last two options: Any convex quadrilateral and Any concave quadrilateral. Square and rectangle are convex quadrilaterals, so setting them out as an option can be interpreted as "only squares and rectangles".

If you choose a kite as outer quadrilateral, you get as inner quadrilateral a rectangle, which is a parallelogram. But a kite need not to be a rectangle or konvex. So all answers are possible.

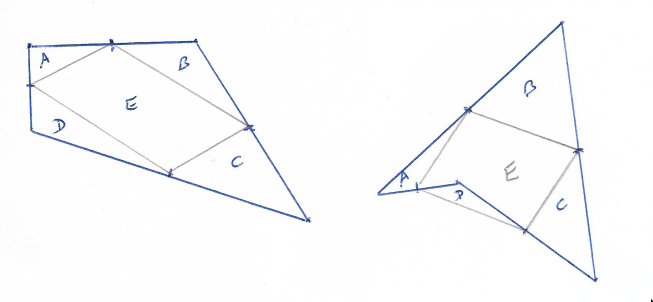
In the first diagram the two triangles A and C can be joined to form a quadrilateral half the size of the original. Similarly B and D can be joined to form the same half-size quadrilateral. Each of these half-size quadrilaterals are 1/4 the area of the original. Hence A+C+B+D = half of Q (where Q is the area of the original quadrilateral) and hence area E = the other half of Q.

For a concave quadrilateral, as per the diagram on the right, the area E still represents the area of the parallelogram but the arithmetic is slightly different. A+C = Q/4 as before. But joining the other two triangles gives B–D = Q/4. Hence A+C+B–D = Q/2. But notice that Q = A+B+C+(E–D) which still gives us Q = E + Q/2 or E = Q/2.

Therefore any quadrilateral, whether convex or concave will yield a parallelogram half its area.

Here is a proof with vectors. It might not be geometric, but it shows that the result holds also for any 4 points in 3D (if you the understand the area of the quadrilateral as the area of two planar triangles which can be made out of the 4 points).

Label the vertices of the quadrilateral $A, B, C \text{ and } D$ (counterclockwise). The midpoints are $A'=M_{AB}, B'=M_{BC}, C'=M_{CD} \text{ and } D'=M_{DA}$ (also counterclockwise). I'm being lazy in that I use the same notation for the points and the vector describing their coordinates. Recall that $A' = M_{AB} = \frac{1}{2} ( A + B )$ , etc... Because $B'-A' = M_{BC} - M_{AB} = M_{CD} - M_{DA} = C'-D'$ the midpoint quadrilateral is a parallelogramm.

Assume without loss of generality that $A$ is the origin (so 0 as a vector). Recall that the [norm of the] cross product gives the area of a parallelogramm spanned by the vectors. The area of this parallelogramm is (in three dimensions, I should add ``the norm of'') $\begin{array}{rl} \overrightarrow{A'B'} \times \overrightarrow{A'D'} & = (B' - A') \times (D' - A')\\ & = B' \times D' - A' \times D' - B' \times A'\\ & = \frac{1}{4} ( B \times D+ C \times D - B \times D - C \times B )\\ & = \frac{1}{4} ( C \times D - C \times B )\\ \end{array}$ Split the quadrilateral into two triangles. Recall that half the [norm of the] cross product gives the area of the triangle spanned by the vectors. Then the area of the original quadrilateral is $\begin{array}{rl} \frac{1}{2} \overrightarrow{AB} \times \overrightarrow{AC} + \frac{1}{2} \overrightarrow{AC} \times \overrightarrow{AD} = \frac{1}{2} ( B \times C + C \times D) \end{array}$ Since $-C \times B = B \times C$ one sees that the parallelogramm has half the area of the quadrilateral.