Shrapnel
A bomb of mass is located at a center of a spherical shell of mass that has two diametrically opposed orifices subtending solid angles and . The bomb explodes, isotropically, into many fragments of equal mass and velocity . If , determine the final velocity of the shell in m/s . Assume that the collisions between the fragments and the shell are perfectly inelastic and ignore gravity.
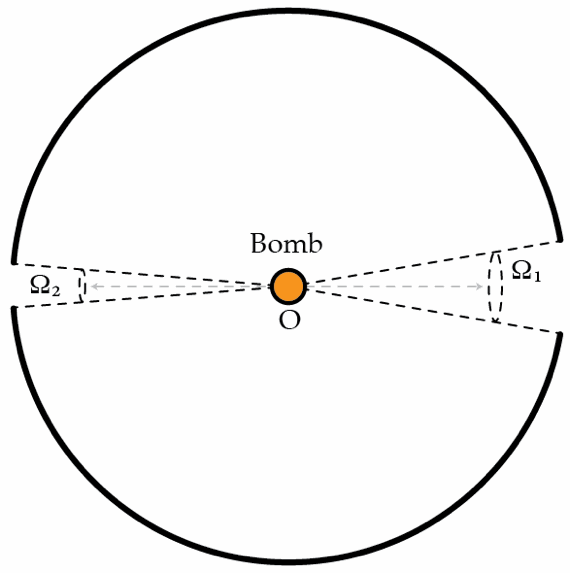
The answer is 5.89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The motion of the shell comes from the imbalance between the two solid angles.
Expand the cone of solid angle Ω 2 such that Ω 1 = Ω 2 . In this case it is clear that the sphere must stay still after the explosion, the reason being that every particle that does hit the shell is perfectly balanced by another particle in the opposite direction.
The symmetry is broken in the problem; on the side of the smaller solid angle, there is an overhang (blue area in the figure below) that catches more material than the side of the larger solid angle which leads to an overall horizontal component of motion. Clearly, the vertical component of momentum delivered to the annulus is zero since the particles are symmetric with respect to the angle ϕ defined below.
The collision is perfectly inelastic, so we know that all bomb material that collides with the surface ends up stuck to it. Let's assume that some amount of momentum is delivered to the overhand Δ p . The mass of the shell plus stuck bomb particulate, M S B is given by
M S B = M S + 4 π M B ( 4 π − π / 2 − π / 3 ) = M B ( 2 − 4 π π / 2 + π / 3 ) = M B 2 4 4 3
Also, by conservation of momentum: Δ p = M S B v S B .
Δ p can be found by summing the horizontal component of momentum for all of the particles that hit the overhang on the blue annulus.
i.e. ∫ d Ω cos θ
If we set up a spherical coordinate system about the center of the large hole, we have θ which measures the angle from the horizontal, and ϕ which measures the angle around the horizontal. We need to know the range of θ for the two solid angles. The solid angle for a spherical patch is equal to
Ω = 2 π 0 ∫ θ ∗ d θ sin θ = 2 π ( 1 − cos θ ∗ )
which we can use to calculate the range of θ to use for the orifices.
We get θ ∗ = cos − 1 4 3 for the solid angle 2 π
and
θ ∗ = cos − 1 6 5 for the solid angle 3 π .
The (horizontal) momentum delivered to the annulus is then
Δ p = v 0 4 π M B 0 ∫ 2 π d ϕ cos − 1 6 5 ∫ cos − 1 4 3 d θ cos θ sin θ = v 0 2 M B cos − 1 6 5 ∫ cos − 1 4 3 d θ cos θ sin θ = v 0 M B 5 7 6 1 9
Putting it all together, we have
v S B = M S B Δ p = v 0 M S B M B 5 7 6 1 9 = v 0 4 3 2 4 5 7 6 1 9 = 1 0 3 2 1 9 v 0 ≈ 5 . 8 9 m/s