Shuffleboard Meets Darts

Classical Mechanics Level 5

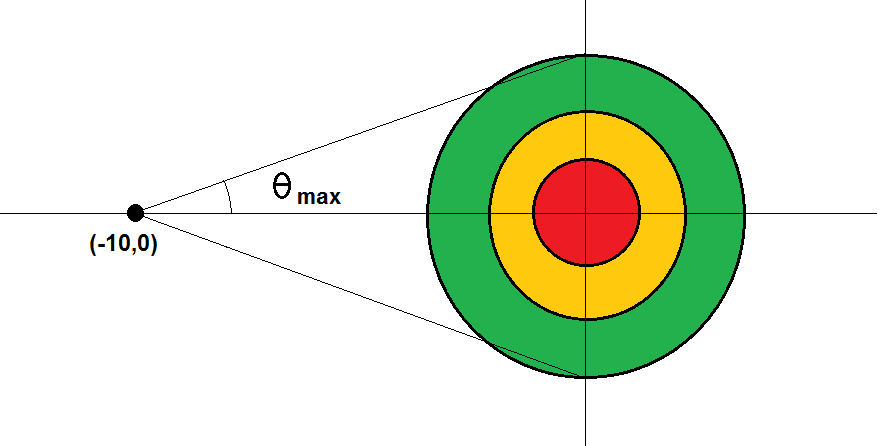
In the $xy$ plane, a target centered on the origin consists of the space between three concentric circles of radii $1$ , $2$ , and $3$ meters. The target has a uniform friction coefficient $\mu = 0.3$ . The region outside the target is friction-less. Gravity $(10 \, \text{m/s}^2)$ is in the $z$ direction (into the page).

A $1 \, \text{kg}$ puck is slid from point $(x,y) = (-10,0)$ with an initial speed $v$ at an angle $\theta$ with respect to the $x$ axis. Let $v_0$ be the speed which would cause the puck to stop exactly at the center of the target for an initial angle $\theta = 0$ . Let $\theta_{max} = \text{atan} \Big (\frac{3}{10} \Big)$ .

Over many trials, the initial speed varies randomly and uniformly in the range $\frac{1}{2} v_0 \leq v \leq \frac{3}{2} v_0$ . The initial angle varies randomly and uniformly in the range $- \theta_{max} \leq \theta \leq +\theta_{max}$ .

If the puck comes to rest within the red region, $3$ points are scored. If the puck comes to rest within the orange region, $2$ points are scored. If the puck comes to rest within the green region, $1$ point is scored. If the puck does not come to rest somewhere on the target, no points are scored.

What is the expected number of points scored by sliding the puck?

The answer is 1.2469.

1 solution

Karan Chatrath
Mar 24, 2019

I am laying out the steps involved to arrive at the correct answer.

The motion of the puck is confined to a straight line. The underlying physics of the problem is fairly straightforward and the value of $v_o$ is:

$\Large{v_o = \frac{3}{\sqrt{5}}}$

Let the initial speed be $\Large{v_i = f_v v_o}$ , where $f_v$ is a factor that varies between 0.5 and 1.5.

The height h can be computed by solving the equation:

$\Large{\frac{h^2}{(\sin(\theta))^2} - \frac{20h}{\tan(\theta)} +91 = 0}$ .

Let the two roots be $h_1$ and $h_2$ .

$\Large{h = min(\mid{h_1}\mid,\mid{h_2}\mid) sign(h_1)}$

Having computed h, k can now be computed as follows:

$\Large{k = -10 + \frac{h}{\tan(\theta)}}$

The stopping distance of the puck is:

$\Large{S = \frac{v_i^2}{2f}}$

The final coordinates of the puck are:

$\Large{x_f = k+S \cos(\theta)}$

$\Large{y_f = h+S \sin(\theta)}$

Finally, we compute the distance between the end coordinates and the origin. That is:

$\Large{R = \sqrt{x_f^2 + y_f^2}}$

According to the question, if the puck stops within the red zone, three points are awarded. Similarly, two points for the orange zone and one for the green zone. This can be coded in the form of if-else conditions based on the value of R.

Between the specified limits of angle and initial velocity, a large 2-D array of points can be computed using this logic. I divided the angle and velocity into a 1000 intervals between the specified limits and computed the points scored for each case.

The expected value is just another term for average and so by taking the average of all terms in the 2D array gives the answer of 1.2451 .

I look forward to seeing an alternate and more rigorous approach to this problem. I was wondering if it is possible to derive a probability density function for points scored, which depends on initial velocity and angle.

Shuffleboard Meets Darts

The answer is 1.2469.

1 solution

0 pending reports