Shuffleboard physics (I)

Classical Mechanics Level 2

Table shuffleboard is a game (usually found in higher quality bars) in which a heavy puck is glided down a long table toward an end zone. Points are scored by getting the puck to come to rest as close to the edge as possible, the closer the puck, the higher the reward.

If the puck slides off the end of the table, however, the player gets zero points. In the table shown below, three points are awarded for the far zone, one for the near zone, and zero if the puck doesn't cross the first line.

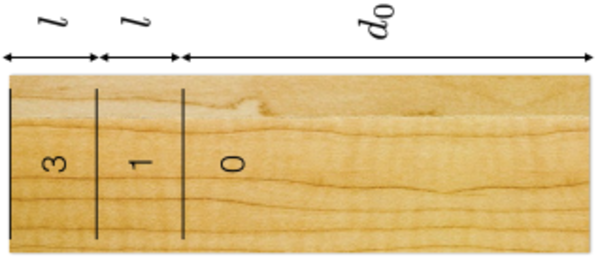
Crudely, the difficulty $D$ of making it into each zone is proportional to $1/\Delta s$ , the range of allowable speeds between which the puck still stop inside the given zone. For example, if the puck is released with speed $s_3^\textrm{max}$ , it will stop just before falling off the end of the table, and if released with speed $s_3^\textrm{min}$ , it will stop just inside the three point zone, and $\Delta s_3 = s_3^\textrm{max} - s_3^\textrm{min}$ .

Suppose the puck and the table have a coefficient of kinetic friction given by $\mu_k$ , and that the puck is pulled down by the acceleration due to gravity, $g$ . How much more difficult is it to get the puck to stop in the three point zone than in the one point zone? In other words, find

$\frac{D_3}{D_1} = \frac{\Delta s_1}{\Delta s_3}$

Details

$d_0=15$ m
$l=5$ m

The answer is 1.13505.

2 solutions

Brian Charlesworth
Oct 10, 2014

The acceleration of the puck along the shuffleboard surface will be $-\mu_{k}g$ no matter what the initial speed is.

Now, using the formula $s_{f}^{2} = s_{o}^{2} + 2ad$ , we set $s_{f} = 0$ to get the distance $d$ the puck will travel until rest for a given initial speed $s_{o}$ .

We thus have the formula $s_{o} = \sqrt{2\mu_{k}gd}$ .

Since the one point zone goes from $15$ to $20$ m we have that

$\Delta s_{1} = \sqrt{2\mu_{k}g}(\sqrt{20} - \sqrt{15})$ ,

and since the three point zone goes from $20$ to $25$ m we have that

$\Delta s_{3} = \sqrt{2\mu_{k}g}(\sqrt{25} - \sqrt{20})$ .

Thus the desired ratio is $\dfrac{\sqrt{20} - \sqrt{15}}{\sqrt{25} - \sqrt{20}} = \dfrac{2 - \sqrt{3}}{\sqrt{5} - 2} = \boxed{1.135}$

to three decimal places.

Good solution, @brian charlesworth

Anuj Shikarkhane - 6 years, 8 months ago

Thanks. :)

Brian Charlesworth - 6 years, 8 months ago

N. Aadhaar Murty
Oct 13, 2020

By, the Work - K.E. theorem, we have

$F_{fric}d = \mu_{k} mgd = \frac {mv^{2}}{2} \therefore v = \sqrt {2\mu_{k} gd}$

for $D_{3}$ , $(d_{min} = 20 \text{m}, d_{max} = 25 \text {m})$ and for $D_{1}$ , $(d_{min} = 15 \text {m}, d_{max} = 20 \text {m})$ .

$\therefore \frac {D_{3}}{D_{1}} = \frac { \sqrt {40\mu_{k} g} - \sqrt {30\mu_{k} g}}{ \sqrt {50\mu_{k} g} - \sqrt {40\mu_{k} g}} = \boxed {1.135}$

Shuffleboard physics (I)

The answer is 1.13505.

2 solutions

0 pending reports