Side Length of Triangle

Use Stewart's theorem, that simplifies the problem.

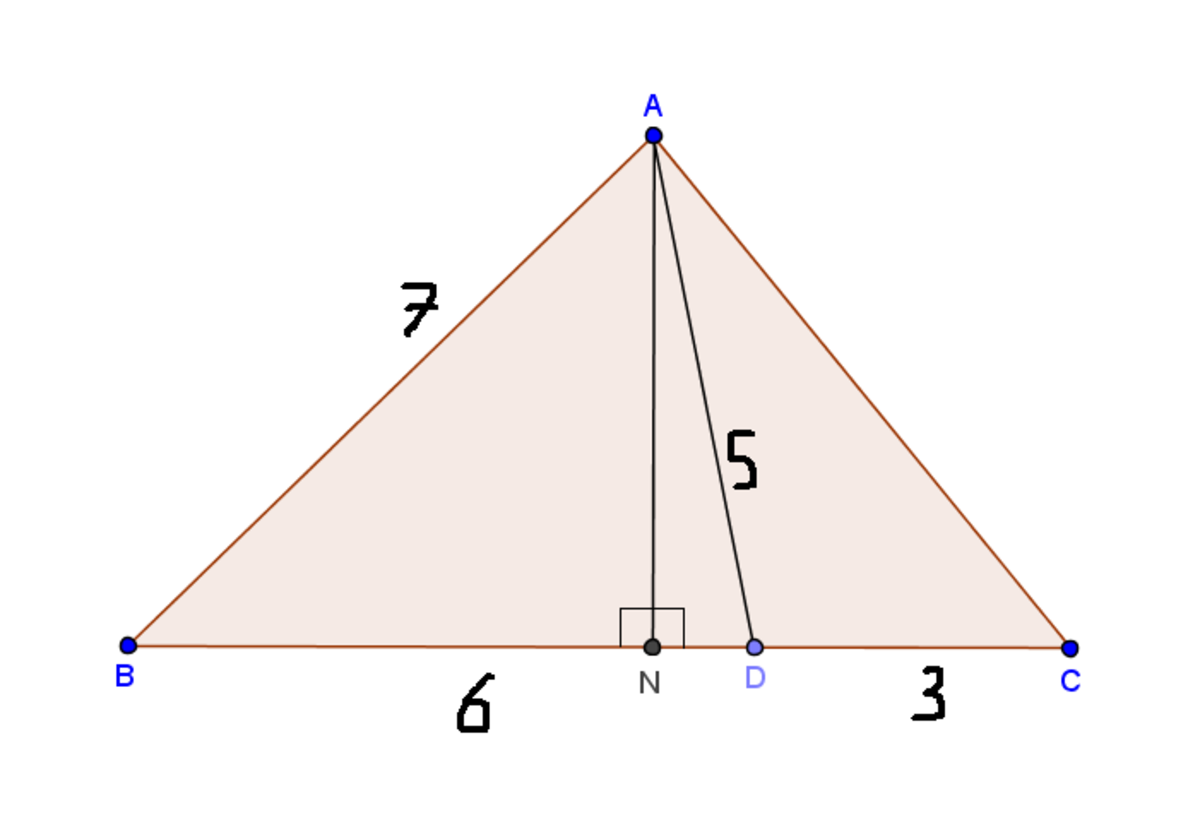
In this diagram, we draw $\Delta ABC$ with the given data and we also draw a normal $AN\perp BC$ . Next, we use Pythagoras Theorem for $\Delta ANB$ and $\Delta AND$ to get the following equations:

$AN^2+BN^2=AB^2\quad,\quad AN^2+ND^2=AD^2 \\ \implies AN^2=AB^2-BN^2=AD^2-ND^2 \\ \implies 49-BN^2=25-ND^2 \\ \implies BN^2-ND^2=24\\ \implies (BN-ND)(BN+ND)=24\\ \implies BD(BN-ND)=24\\ \implies BN-ND=\dfrac{24}{BD}=\dfrac{24}{6} \implies BN-ND=4 \ldots (i)$

Also, we have,

$BC=BN+ND=BD+DC=6+3 \implies BN+ND=9 \ldots (ii)$

Solving $(i)$ and $(ii)$ , we get $BN=5~,~ND=1$ .

Now, using Pythagoras Theorem for $\Delta ANC$ , we have,

$AN^2+NC^2=AC^2\\ \implies (AD^2-ND^2)+(ND+DC)^2=AC^2\\ \implies AC^2=(25-1)+(1+3)^2=24+16 \implies \boxed{AC^2=40}$

Let $\angle ABC = \theta$ . Using Cosine Rule, we have:

$\quad AD^2=AB^2+BD^2-2(AB)(BD)\cos{\theta}$

$\quad\Rightarrow 5^2 = 7^2 + 6^2 -2(7)(6)\cos{\theta}\quad \Rightarrow 84\cos{\theta} = 60\quad \Rightarrow \cos{\theta} = \frac {5}{7}$

Also,

$\quad AC^2=AB^2+BC^2-2(AB)(BC)\cos{\theta}$

$\quad\Rightarrow AC^2 = 7^2 + 9^2 -2\times 7\times 9\times \dfrac {5}{7} = 130 - 90 = \boxed{40}$