Side Squared
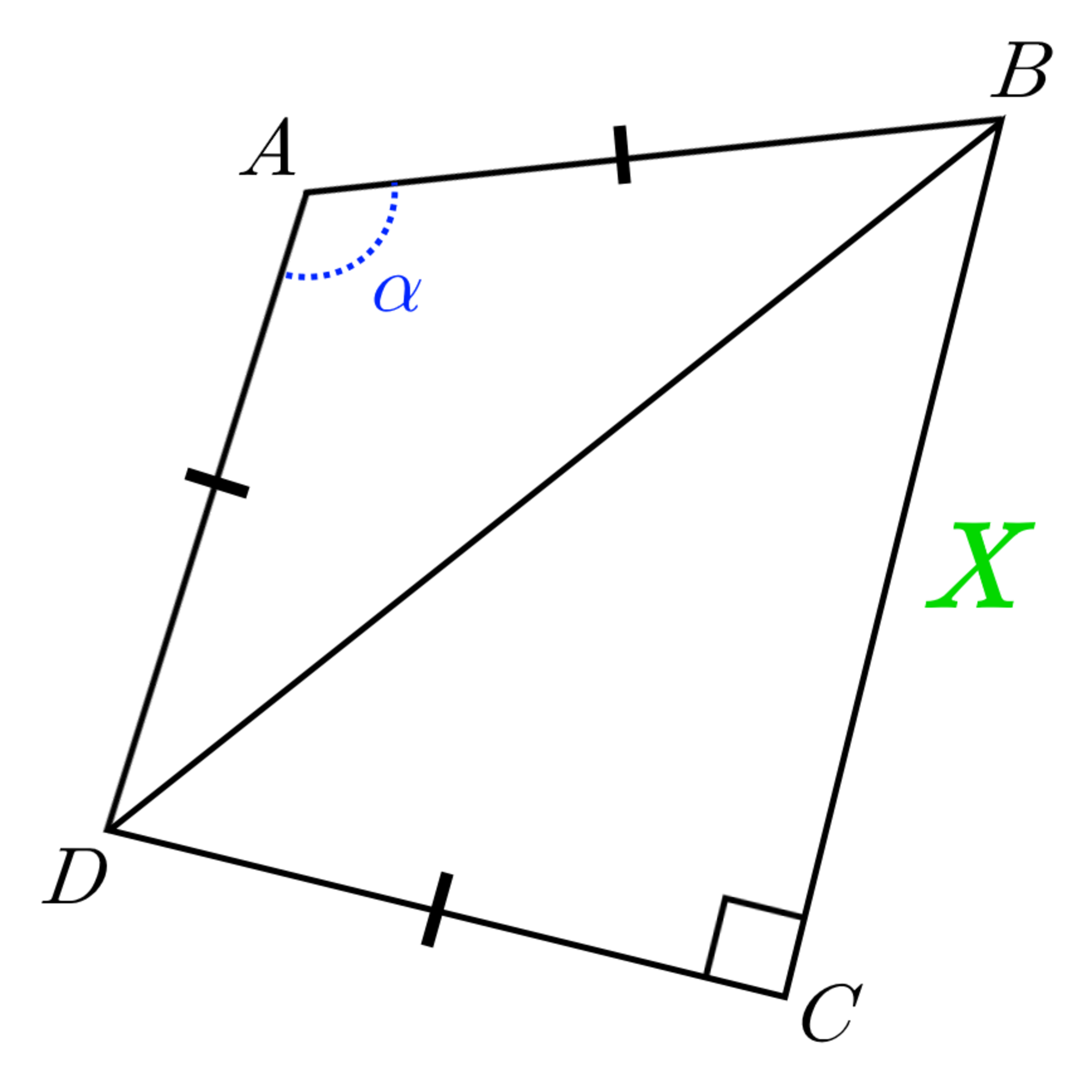 A
B
C
D
is a quadrilateral where
A
B
=
A
D
=
C
D
=
l
.
△
B
C
D
is right. It is given that
B
C
=
X
=
l
2
. By considering
α
, or otherwise, find the set of all possible values of
X
.
A
B
C
D
is a quadrilateral where
A
B
=
A
D
=
C
D
=
l
.
△
B
C
D
is right. It is given that
B
C
=
X
=
l
2
. By considering
α
, or otherwise, find the set of all possible values of
X
.
Input a + b as your answer, where a < X < b .
The answer is 3.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
A simpler solution:
We know that B D = l 2 + l 4 .
In any given triangle, the sum of two sides is always greater than the remaining side.
Thus, l + l > l 2 + l 4 ⟹ ( 2 l ) 2 > l 2 + l 4 ⟹ 3 l 2 > l 4 ⟹ 3 > l 2 .
Quite clearly, for smaller values of l we have l 2 approaching 0.
Since X = l 2 , 0 < X < 3 ⟹ a + b = 3 .
Maximum value is at α = π :
l 2 + l 4 = 4 l 2 → X m a x = l 2 = 3 (Pythagorean theorem)
Minimum value is at α = 0 :
l = 0 → X m i n = 0
3 − 0 = 3
You are right that 0 < X < 3 , however your reasoning for the minimum value is slightly off. In my solution I show that X = l 2 = 1 − 2 cos α , so we must have 1 − 2 cos α ≥ 0 as l 2 is non-negative. This rules out the possibility of α = 0 .
Log in to reply
Ah, fair enough... Nice problem!
But wait a sec... It seems to me that l and X can equal zero without α equaling zero, no?
Log in to reply
l and X will approach zero as α approaches its smallest possible value of 3 π - the quadrilateral tends to a very tiny equilateral triangle! Try making the weak inequality I posted an equality and solve for α .
Relevant wiki: Solving Triangles - Problem Solving - Medium
Firstly note that B D = l 2 + l 4 .
Using the cosine rule on △ A B D , we get l 2 + l 4 = 2 l 2 − 2 l 2 cos α ⇒ l 2 = 1 − 2 cos α = X ( ∗ ) The maximum value of X is max ( 1 − 2 cos α ) = 3 when α = π . This occurs as the quadrilateral tends to a right triangle with hypotenuse D A B side 2 l .
As X = l 2 ≥ 0 , its minimum value is 0 . This occurs as the quadrilateral tends to an equilateral triangle of side l . We can substitute α = 3 π into ( ∗ ) to check.
Thus 0 < X < 3 ⇒ a + b = 3 .