Sidereal Times
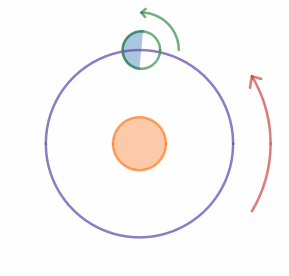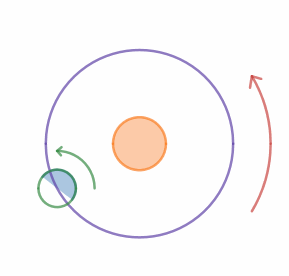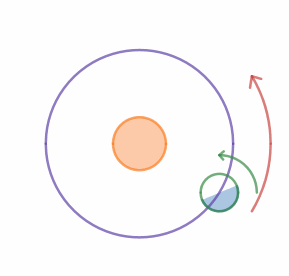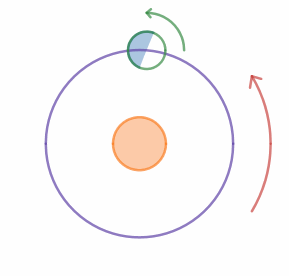
George and Harold are traveling to the equator for the weekend. They measure the length of the shadow cast by George during the day. They start a stopwatch when George's shadow is the shortest on Saturday, and they stop it when George's shadow is the shortest on Sunday.
Let the time duration recorded by the stopwatch be and let be the time it takes for Earth to make one complete rotation about its axis.
How does compare with
Note: Use the fact that Earth rotates about its axis and revolves around the Sun in the same sense. In the animation, both are counterclockwise.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
This is only a guess!
As shown in the figure, the earth not only rotates on it's axis but also around the sun. Let the event that the 'lighter side of the earth faces the sun' in the figure denote shortest shadows. As you may notice, when the earth completes one exact rotation (about its axis), the lighter side returns to its original position with respect to the ground frame, but since it also goes around the sun in the same direction, the earth has to rotate a little further for the lighter side to face the sun , which would take more time than the time of the day, T .
t would have been lesser than T if the directions of both rotations were opposite.