Sides & Angles
 Given here is a
ABC, Its known that
,
& Area of this triangle is 3 square units. Find the length of base BC (d) of this triangle.
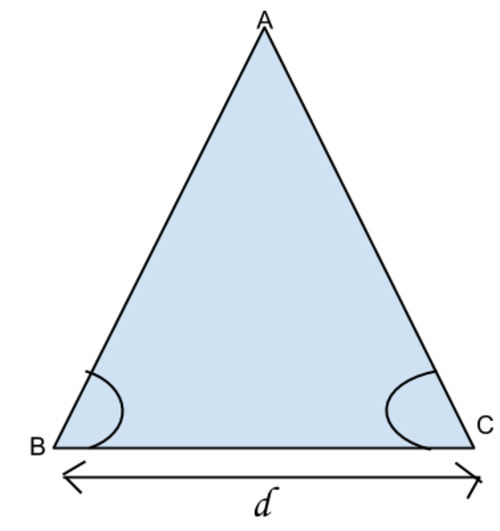
Given here is a
ABC, Its known that
,
& Area of this triangle is 3 square units. Find the length of base BC (d) of this triangle.
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Area = 2 1 × B a s e × H e i g h t
thus, 3 = 2 1 × d × h ...(i) {where h is height of triangle}
tan ( θ ) = b a s e h e i g h t
thus, 2 3 = p h ...(ii) [where p is distance of foot of perpendicular (dropped from A on BC) from B]
And, 2 1 = d − p h ...(iii)
from (ii) & (iii) eliminate p, to get, h = 8 3 d ... (iv)
now use (iv) in (i),
3 = 2 1 × d 2 × 8 3
thus finally, we get answer, d = 4
ALTER:
Move this triangle to cartesian plane & follow simple coordinate geometry. (with BC along positive x - axis.) use: slope = tan θ where θ is angle with positive x-axis.